TS Chimie Spectrophotométrie Cinétique

Page 1 sur 5
Spectrophotométrie Document : M.Moppert - CPF - Beyrouth
TS
Chimie
Spectrophotométrie
Cinétique
Enoncé
On veut étudier la cinétique de l’oxydation des ions iodure I – par le peroxyde d’hydrogène (eau
oxygénée) H2O2. Cette réaction est lente et totale.
A. Etude de la réaction
Les couples d’oxydoréduction mis en jeu sont : H2O2 /H2O et I2 / I -.
L’équation bilan de la réaction étudiée est : H2O2 (aq) + 2 H +(aq) + 2 I –(aq) = 2 H2O + I2 (aq)
Ecrire les demi équations correspondant aux couples mis en jeu.
B. Etude de la cinétique de la réaction par spectrophotométrie
On réalise le mélange ci-dessous (l’eau oxygénée est introduite à la date t = 0) :
Acide sulfurique
c1 = 1,0 mol.L- 1
Solution d’iodure
de potassium
c2 = 1,0 x 10-1 mol.L- 1
Eau oxygénée
c3 = 7,8 x 10-2 mol.L-1
Mélange (a)
V1 = 10 mL
V2 = 18 mL
V3 = 2,0 mL
1. Le mélange réactionnel devient jaune orangé puis brunit peu à peu. Quelle est l’espèce
chimique responsable de cette coloration ?
2. L’évolution de la réaction est suivie par spectrophotométrie dont le principe est décrit ci-
dessous :
« Une lumière monochromatique, de longueur d’onde m et d’intensité lumineuse Io, traverse une
cuve transparente de longueur l contenant une solution colorée de concentration c en matière
colorante.
Une partie de l’intensité lumineuse est absorbée par la solution, l’intensité lumineuse transmise It
est plus faible que l’intensité incidente Io. Ce phénomène d’absorption d’une partie de la lumière
par la solution colorée est caractérisée par une grandeur appelée absorbance A (sans unité).
L’expérience montre que, pour une solution peu concentrée en substance absorbante,
l’absorbance A est, à une température donnée, pour une longueur d’onde donnée, proportionnelle à
la concentration de l’espèce colorante. Le spectrophotomètre permet la mesure de l’absorbance
de la solution colorée. »
A l’aide du
spectrophotomètre,
on a mesuré
l’absorbance A d’une
solution de diiode à
différentes longueurs
d’onde . On obtient
alors le spectre
d’absorption  A()
ci-dessous à gauche :

Page 2 sur 5
Spectrophotométrie Document : M.Moppert - CPF - Beyrouth
a) Sur quelle longueur d’onde m va-t-on régler la source du
spectrophotomètre ?
b) La valeur de m trouvée confirme-elle la réponse apportée à la
question B.1 ? Utiliser le document ci-dessus à droite pour
répondre (chaque couleur absorbe dans le domaine de longueur
d’onde indiqué et deux couleurs complémentaires se font face).
3. On suit l’évolution de l’absorbance du mélange réactionnel ci-dessus en éclairant la cuve
contenant quelques millilitres du mélange, avec une lumière monochromatique de longueur
d’onde m.
On peut ainsi tracer, en annexe 1, le graphe représentatif de la fonction t  A(t).
a) Pourquoi l’absorbance augmente-t-elle au cours du temps ?
b) Pourquoi l’absorbance est-elle constante lorsque t est supérieur à 1000 s ?
c) Quels arguments permettent d’affirmer : « Le temps de demi-réaction est le temps au bout
duquel l’absorbance atteint la moitié de sa valeur finale » ?
d) En utilisant cette affirmation, déterminer graphiquement le temps t½ de demi-réaction.
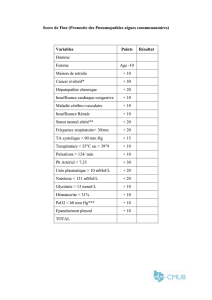
4. A partir des résultats expérimentaux on déduit, en annexe 2, le graphe représentatif de la
fonction t  [I2](t).
a) Définir la vitesse volumique instantanée de formation du diiode à la date t.
b) Déterminer graphiquement sa valeur à la date t = 0 et à la date t½.
c) Justifier la variation de cette vitesse au cours du temps.
d) Quelle sera la vitesse de disparition de l’eau oxygénée aux mêmes dates ?
e) Compléter numériquement, en annexe 3, le tableau descriptif de l’évolution du système.
f) En déduire le réactif limitant et calculer la concentration en diiode formé quand la réaction
est terminée.
g) Vérifier cette valeur sur la courbe de l’annexe 2. La réaction est-elle terminée ?
5. On recommence l’expérience avec le mélange suivant :
Acide sulfurique
c1 = 1,0 mol.L- 1
Solution d’iodure
de potassium
c2 = 1,0 x 10-1 mol.L- 1
Eau oxygénée
c3 = 7,8 x 10- 2 mol.L-1
Eau
distillée
Mélange (b)
V1 = 10 mL
V’2 = 10 mL
V3 = 2,0 mL
V4 = 8,0 mL
a) A la date t = 0, la vitesse de formation du diiode dans le mélange (b) est-elle plus petite,
égale ou plus grande que la vitesse de formation du diiode dans le mélange (a) ?
b) A la date t infinie, la concentration en diiode formé dans le mélange (b) est-elle plus petite,
égale ou plus grande que la concentration en diiode formé dans le mélange (a) ?

Page 3 sur 5
Spectrophotométrie Document : M.Moppert - CPF - Beyrouth
Annexes
ANNEXE 1
ANNEXE 2
[I2] (mmol/L)
ANNEXE 3
Réaction
H2O2 (aq) + 2 H+(aq) + 2 I-(aq) = 2 H2O + I2 (aq)
Date
Avancement
(mmol)
Quantité
de H2O2(aq)
(mmol)
Quantité
de H+(aq)
(mmol)
Quantité
de I-(aq)
(mmol)
Quantité
de H2O
(mmol)
Quantité
de I2(aq)
(mmol)
t = 0
excès
excès
t
excès
excès
t
excès
excès

Page 4 sur 5
Spectrophotométrie Document : M.Moppert - CPF - Beyrouth
Corrigé
A. Ecrire les demi équations correspondant aux couples mis en jeu.
2 H+ + 2 e- + H2O2 = 2 H2O
2 I- = I2 + 2 e-
_______________________________
H2O2 (aq) + 2 H +(aq) + 2 I –(aq) = 2 H2O + I2 (aq)
B. 1. Le mélange réactionnel devient jaune orangé puis brunit peu à peu. Quelle est l'espèce chimique responsable
de cette coloration ?
C'est le diiode I2 qui est responsable de la coloration.
2. a) Sur quelle longueur d’onde m va-t-on régler la source du spectrophotomètre ?
On va régler la source du spectrophotomètre sur la longueur d’onde m = 475 nm qui correspond
au maximum d’absorption du diiode.
b) La valeur de m trouvée confirme-elle la réponse apportée à la question B.1 ?
La valeur trouvée correspond à l’absorption de la radiation bleu ce qui explique la couleur orangée
(complémentaire du bleu) du diiode.
3. a) Pourquoi l'absorbance augmente-t-elle au cours du temps ?
Car la concentration en diiode augmente au cours du temps et, de ce fait, la coloration brune
également.
b) Pourquoi l'absorbance est-elle constante lorsque t est supérieur à 1000 s ?
Car la réaction est terminée.
c) Quels arguments permettent d'affirmer : "Le temps de demi-réaction est le temps au bout duquel l'absorbance
atteint la moitié de sa valeur finale" ?
Le temps de demi-réaction est la durée au bout de laquelle l’avancement atteint la moitié de sa
valeur finale. Si on note x l’avancement, on remarque qu’il est égal à la quantité de matière d’eau
oxygénée consommée ou à la quantité de diiode formé. Comme l’absorbance A ( …) est
proportionnelle à la concentration de l’espèce colorante (cf. énoncé), on en déduit que le temps de
demi-réaction est la durée au bout de laquelle l’absorbance atteint la moitié de sa valeur finale.
d) En utilisant cette affirmation, déterminer graphiquement le temps t½ de demi-réaction.
Amax = 1,1 => A1/2 = 0,55 => (par lecture graphique) t1/2 = 150 s
4. a) Définir la vitesse volumique instantanée de formation du diiode à la date t.
C'est la valeur de la dérivée de la concentration en diiode par rapport au temps à la date
considérée.
b) Déterminer graphiquement sa valeur à la date t = 0 et à la date t½.
Les vitesses cherchées sont égales aux coefficients directeurs des tangentes à la courbe
représentative de la fonction t  [I2](t) aux dates considérées.
On trouve : v(I2)0  2,5 x 10-2 mmol.L-1.s-1 et v(I2)1/2  1,0 x 10-2 mmol.L-1.s-1
c) Justifier la variation de cette vitesse au cours du temps.
Au fur et à mesure de l’avancement de la réaction, la concentration des réactifs diminue et donc
la vitesse de la réaction diminue.
d) Quelle sera la vitesse de disparition de l'eau oxygénée aux mêmes dates ?
La vitesse de disparition de l'eau oxygénée aux mêmes dates sera la même que la vitesse
d'apparition du diiode. En effet, dans le même temps, la quantité de diiode qui apparaît est égale
à la quantité d'eau oxygénée qui disparaît (cf. coefficients stoechiométriques).

Page 5 sur 5
Spectrophotométrie Document : M.Moppert - CPF - Beyrouth
e) Compléter numériquement, en annexe 3, le tableau descriptif de l’évolution du système.
Réaction
H2O2 (aq) + 2 H+(aq) + 2 I-(aq) = 2 H2O + I2 (aq)
Date
Avancement
(mmol)
Quantité
de H2O2 (aq)
(mmol)
Quantité
de H+(aq)
(mmol)
Quantité
de I-(aq)
(mmol)
Quantité
de H2O
(mmol)
Quantité
de I2(aq)
(mmol)
t = 0
0
1,6.10-1
Excès
1,8
Excès
0
t
x
1,6.10-1 - x
Excès
1,8 – 2x
Excès
x
t
xmax =1,6.10-1
0
Excès
1,5
Excès
1,6.10-1
f) En déduire le réactif limitant et calculez la concentration en diiode formé quand la réaction est terminée.
On remarque que n(H2O2)0 <
0
n(I )
2
: l’eau oxygénée est le réactif limitant.
[I2]max =
2 max
n(I )
V
soit [I2]max =
4
3
1,6 10
30 10
= 5,3 x 10-3 mol.L-1 ou 5,3 mmol.L-1
g) Vérifier cette valeur sur la courbe de l’annexe 2. La réaction est-elle terminée ?
Par lecture graphique on voit que : [I2]max  5,3 mmol.L-1 : la réaction est bien terminée.
5. a) A la date t = 0, la vitesse de formation du diiode dans le mélange (b) est-elle plus petite, égale ou plus
grande que la vitesse de formation du diiode dans le mélange (a) ?
Elle est plus faible puisque la concentration en ions iodure est plus faible.
b) A la date t infinie, la concentration en diiode formé dans le mélange (b) est-elle plus petite,égale ou plus
grande que la concentration en diiode formé dans le mélange (a) ?
On vérifie que l'eau oxygénée est toujours le réactif limitant et on remarque que la
concentration initiale d'eau oxygénée n'a pas changé. On a donc toujours : [I2]max = [H2O2]0 et, de
ce fait, la concentration en diiode formé reste la même.