Exercice n° 1 - PhysiqueWeb2

Page 1 sur 5
REPUBLIQUE TUNISIENNE
MINISTERE DE L’EDUCATION
SCIENCES PHYSIQUES
REVISION
EXAMEN DE BACCALAUREAT
Année scolaire : 2011-2012
www.physiqueweb2.c4.fr

Page 2 sur 5
LYCEE ZAHROUNI-TUNIS-
SCIENCES PHYSIQUES
4ème MATH
Révision 1
Chimie : Réaction d’estérification Physique : circuit LC
Loi d’action de masse
CHIMIE
CHIMIE
A t=0 s et à une température constante , On mélange un volume V1 d’une solution (S1) de
péroxodisulfate de potassium K2S2O8 de concentration molaire C1 et un volume V2 d’une solution
(S2) d’iodure de potassium KI de concentration molaire C2, avec C2=2 C1.
1- Écrire les équations des deux demi-réactions, déduire l’équation bilan.
2- A l’instant t=0, le mélange des deux solutions, de volume total V= 1 L, contient n01=10mmol
d’ions peroxodisulfate et n02=20 mmol d’ions iodures.
a- Dresser le tableau d’évolution du système chimique.
b- Déterminer [S2O82-]0 et [I-]0, concentrations molaires initiales respectives des ions
peroxodisulfates et les ions ions iodures dans le mélange. Déduire C1 et C2.
3- A la date t=0, on divise le mélange précédent en 10 prélèvements identiques. Pour déterminer la
quantité de matière de diiode formé à une date t>0, on refroidit l’un des prélèvements en y
versant de l’eau glacée puis on dose le diiode formé par une solution de thiosulfate de sodium
(Na2S2O3) de concentration molaire C3=4.10-2 mol.L-1.
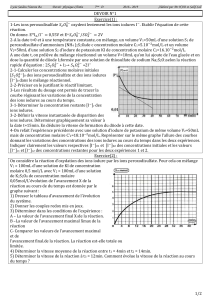
La réaction de dosage, rapide et totale, est 2S2O32- + I2  S4O62- +2I- ce qui a permis de tracer la
courbe de variation de la concentration molaire de diiode en fonction du temps (voir fig 1).
a- Pourquoi refroidit-on chaque prélèvement ? quel(s) facteur(s) cinétique(s) met on en évidence ?
b- Calculer le volume V3 de la solution de thiosulfate de sodium nécessaire pour doser la quantité
de diiode I2 formé dans un prélèvement à la date t2=40 min.
4- Calculer la concentration molaire théorique de diiode à la fin de la réaction. Ce résultat est il
en accord avec le résultat expérimental ?
5- Calculer en mmol.L-1.min-1 :
a- La vitesse volumique moyenne (Vvol)moy de la réaction entre les dates t1=0 et t2=40 min.
b- La vitesse volumique à la date t2=40 min.
6- On répète l’expérience précédente à la même température mais avec une concentration en
ions peroxodisulfate plus grande, tracer, sur le même graphe, l’allure de la courbe de variation
de la concentration de diiode au cours du temps.
0
2
t(min)
[I2] (mmol.L-1)
4
6
8
10
4
0
8
0
Fig 1
REPUBLIQUE TUNISIENNE
MINISTERE DE L’EDUCATION
EXAMEN DE BACCALAUREAT
SECTION : MATHEMATIQUE
EPREUVE : SCIENCE PHYSIQUE
CHIMIE : Cinétique chimique
PHYSIQUE : RC-RLC
4

Page 3 sur 5
PHYSIQUE
On se propose de déterminer la capacité d’un condensateur à partir de deux méthodes différentes.
On dispose du matériel suivant :
- un générateur de tension continue E = 20 V ;
- une boîte de résistances étalonnées R ( 1 Ω , 10 Ω , 100 Ω ,1000 Ω) ;
- une bobine idéale d’inductance L = 0,50 H et de résistance nulle ;
- un condensateur de capacité C inconnue ;
- un ordinateur relié au montage par une interface et permettant d’enregistrer
des variations de tensions et d’intensité au cours du temps ;
- des fils de connexion sécurisés ;
- un interrupteur.
I - Première méthode.
Le montage d’un circuit RC est représenté sur la figure 1.
À l’aide de l’ordinateur, on enregistre les variations, au cours du temps
des deux tensions u1 et u2 à partir de l’instant de la fermeture de
l’interrupteur, choisi comme origine des dates.
Les graphes obtenus pour les différentes valeurs de la résistance R
sont reproduits sur l’annexe 3,
1. Compléter le tableau de l’annexe 3, en indiquant dans chaque case, le numéro de la courbe qui
convient (le même numéro peut apparaître plusieurs fois).
2. Compléter le tableau de l’annexe 4 après avoir déterminé graphiquement la constante de temps τ
correspondant à la charge du condensateur pour R = 1600 Ω en expliquant la méthode utilisée.
3. Donner l’expression de la constante de temps τ en fonction des caractéristiques du circuit. Justifier
son unité par une analyse dimensionnelle.
4. Tracer sur l’annexe 5, le graphe représentant τ en fonction de R
(échelle : 1 carreau ↔ 0,02 s et 1 carreau ↔ 100 Ω).
En déduire la valeur de C en expliquant la méthode utilisée.
II - Deuxième méthode.
Le condensateur chargé sous une tension E = 20 V
est maintenant placé en série avec la résistance R et
la bobine idéale d’inductance L = 0,50 H et de
résistance nulle.
Le circuit ainsi réalisé est représenté sur la figure 2.
À l’instant de date t = 0 s, on ferme l’interrupteur.
L’ordinateur permet de suivre les variations, au cours
du temps de la tension uC et de l’intensité i.
R
i
u1
u2
E
C
Figure 1
R
i
L
uL
uC
C
uR
Figure 2

Page 4 sur 5
1. On donne ci-dessous plusieurs courbes représentant les variations de uC au cours du temps pour
différentes valeurs de R.
Compléter le tableau de l’annexe 6, en associant chaque courbe à la valeur de R qui lui correspond et
donner le nom du régime de décharge.
2. Établir l’équation différentielle vérifiée par la fonction uC (t) si la résistance R est nulle.
3. L’ordinateur donne la courbe suivante :
a. Déterminer la période propre T0 des oscillations et donner son expression en fonction des
caractéristiques du circuit.
b. En déduire la valeur de C.
On donne :
(0,060)2 = 3,610 –3 π2 ≈ 10

Page 5 sur 5
Annexe 3
R ()
400 
800 
1200 
1600 
Courbe
représentant u1
Courbe
représentant u2
Annexe 4
R (Ω)
400 Ω
800 Ω
1200 Ω
1600 Ω
τ (s)
0,06
0,14
0,21
Annexe 5
Annexe 6
R= 2 Ω
R= 10 Ω
R= 1000 Ω
Courbe représentant uC
Nom du régime de
décharge
Échelle :
1 carreau  0,02 s
1 carreau  100 
R ()
 (s)
t (s)
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
u1(V)
5
10
15
20
u2 (V)
25
0
0
5
4
3
2
1