Le 13/12/2013 Page : 1 / 4 Devoir type Bac - Correction TS

13/12/2014 Devoir_commun2013_1_corr.doc 1/4
Le 13/12/2013
Page : 1 / 4
Devoir type Bac - Correction
Tale S
I. L’ibuprofène (7 points)
1. La molécule d’ibuprofène
1.1. La molécule appartient aux acides carboxyliques
1.2. La formule brute de l’ibuprofène est C13H18O2.
1.3. M(C13H18O2) = 13  M(C) + 18  M(H) + 2  M(O) = 13  12,0 + 18  1,0 + 2  16,0 = 206 g.mol-1
M 210 g.mol-1 (2 chiffres significatifs)
1.4. Une capsule de médicament contient 500 mg d’ibuprofène.
La quantité d’ibuprofène est n = m
M ; Soit un nombre de molécules N = NA  m M
N = 6,02  1023  0,400
210 = 1,1  1021
2. Synthèse de l’ibuprofène par le procédé BOOTS
2.1. Par conservation des éléments chimiques, la molécule A a pour formule brute C2H4O2. La molécule d’acide
éthanoïque CH3  COOH a la même formule brute donc A peut correspondre
à l’acide éthanoïque.
2.2. Formule développée de l’acide éthanoïque ci-contre :
2.3. Le méthanoate de méthyle a la même formule brute que l’acide éthanoïque
donc le méthanoate de méthyle et l’acide éthanoïque sont des isomères.
2.4. Le spectre de l’acide éthanoïque a un pic large de forte intensité vers 3200-
3650 cm-1 caractéristique d’un acide carboxylique. Le méthanoate de méthyle est un ester. Donc le spectre de
l’acide éthanoïque est le spectre IR 1.
3. Etude du produit de synthèse par le procédé BOOTS
3.1. Il faut calculer le nombre d’ondes correspondant à λ = 5,80 µm. Or  = 1
 = 1 5,80  10-6 m = 1 5,80  10-4 cm
1700 cm-1. Sur le Doc.3, un pic d’absorption a lieu un peu au-delà de 1700 cm-1. La molécule
d’ibuprofène peut absorber la radiation de longueur d’onde λ = 5,80 µm.
3.2. Le déplacement chimique du signal (g) proche de 12 ppm indique que c’est un proton d'un acide
carboxylique.
3.3. (g) : singulet : ce proton n'est couplé avec aucun autre proton, il n'y a donc aucun « proton proche voisin ».
3.4. L'aire du doublet (a) est environ 6 fois plus grande que l'aire du pic (g). L'aire du doublet indique la présence
de 6 protons. Le déplacement chimique proche de 1 ppm est compatible avec deux groupes méthyle CH3.
3.5. (a) : doublet : ces protons équivalents sont couplés avec un seul autre proton (un seul proton « proche
voisin »).
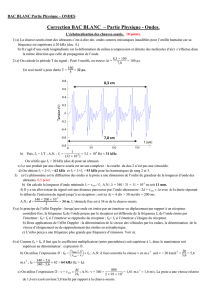
C
CH
CH
CH
CH
C
CH2
CH
CH3
CH3
CH
CH3
COH
O
g
a
C
CH
CH
CH
CH
C
CH2
CH
CH3
CH3
CH
CH3
COH
O
groupe carboxyle
C C
O
O
H
H
H
H

13/12/2014 Devoir_commun2013_1_corr.doc 2/4
4. Synthèse de l’ibuprofène par le procédé BHC
4.1. Les catalyseurs permettent d’accélérer la réaction sans être consommés lors de la réaction. D’autre part, ils
sont spécifiques à une réaction donnée.
4.2. La catalyse utilisée est une catalyse hétérogène. Le catalyseur est solide alors que les réactifs sont dans un
autre état physique.
4.3. Il existe la catalyse homogène, la catalyse enzymatique (le catalyseur est une enzyme c'est-à-dire une
protéine).
II. L’écholocalisation des chauves-souris (8 points)
1) a) Un ultrason est une onde mécanique inaudible pour l’oreille humaine car sa fréquence est supérieure à 20 kHz.
b) Il s’agit d’une onde longitudinale car la déformation du milieu (compression et détente des molécules d’air)
s’effectue dans la même direction que celle de propagation de l’onde.
2) a) On calcule la période T du signal : Pour 5 motifs, on trouve Δt = 8,3 × 150
7,8 = 160 µs.
Un seul motif a pour durée T = 160
5 = 32 µs.
b) f1 = 1
T ; A.N. : f1 = 1
(32  10-6) = 3,1  104 Hz ≈ 31 kHz. On vérifie que f1 > 20 kHz pour un ultrason.
c) On obtient f2 = 2×f1 = 62 kHz et f3 = 3×f1 = 93 kHz pour les harmoniques de rang 2 et 3.
3) a) Ce phénomène est la diffraction des ondes si la proie a une dimension de l’ordre de grandeur de la longueur
d’onde des ultrasons.
b) On calcule la longueur d’onde minimale λ = c / f1 A.N.: λ = 340 / 32.103 = 10,6 mm ≈ 11 mm.
4) a) Voir schéma ci-contre. La chauve-souris détermine
« la durée » que met l’onde ultrasonore pour aller sur
le mur et en revenir et en déterminer la distance d.
b) Il y a un aller-retour du signal soit la distance
parcourue par l’onde ultrasonore 2d = vson  Δt avec
Δt la durée séparant le début de l’émission du signal
jusqu’à sa réception ; soit ici Δt = 4 × 50 = 200 ms.
A.N.: d = 340 × 200  10-3
2 = 34 m. Le mur est à 34 m de la chauve-souris.
5) a) Les ailes de la proie se rapprochent, puis s’éloignent de la chauve-souris, ce qui produit un décalage Doppler de
la fréquence reçue par la chauve-souris ; de plus, ce mouvement étant périodique, ce décalage est oscillant, c’est
à dire alternativement plus grand et plus petit.
b) Les applications de l’effet Doppler sont la mesure de la vitesse des véhicules par les radars (microondes), de la
vitesse d’éloignement des étoiles en astrophysique (visible)...
d
8,3 cm
7,8 cm

13/12/2014 Devoir_commun2013_1_corr.doc 3/4
c) L’écho perçu a une fréquence plus grande car la longueur d’onde diminue (baisse de la distance parcourue par
les ultrasons) ; or f = c / λ, donc si λ diminue, alors f augmente.
6) a) Comme fR > f0, il faut que le coefficient multiplicateur (entre parenthèses) soit supérieur à 1, donc le numérateur
soit supérieur au dénominateur : expression .
b) On utilise l’expression  : fR = 
vson + v
vson - v  f0 ; A.N: il faut convertir la vitesse v en m.s-1
soit v = 20 km.h-1 = 20
3,6 = 5,6 m.s-1 ; fR = 340 + 5,6 340 - 5,6  (62  103) = 64  103 Hz = 64 kHz (fR > f0).
c) On utilise l’expression  : v = vson  f
2f0 ; A.N.: v = 340 × 880
2  93  103 = 1,61 m.s-1 ≈ 1,6 m/s. La proie a une
vitesse relative de 1,6 m/s (soit environ 5,8 km/h) par rapport à la chauve souris.
d) La chauve-souris, se déplaçant à 1,6 m/s par rapport à sa proie, elle mettra une durée t = d
v ;
A.N. : t = 8,5
1,6 = 5,3 s pour la rattraper.
III. Solution de Lugol (5 points)
 Introduction du sujet : Déterminer la masse de I2 présent dans la solution étudiée grâce à l’avancement maximal de
la réaction et expliquer le rôle du zinc et de la lumière sur la cinétique de décomposition du diiode.
 Equation bilan : Le diiode réagit avec le zinc solide selon l’équation bilan : I2 (aq) + Zn (s) → 2 I- (aq) + Zn2+(aq)
 Suivi spectrophotométrique : Au cours de la réaction, le diiode brun (réactif) disparait et il se forme des ions
incolores : la solution devient de moins en moins coloré. On peut donc suivre l’évolution temporelle de cette
réaction par suivi spectrophotométrique en mesurant l’absorbance A de la solution au cours du temps (voir
tableau). D’après la loi de Beer-Lambert, l’absorbance est proportionnelle à la concentration molaire en espèce
colorée (ici au diiode), c’est pourquoi la valeur de A baisse au cours du temps (voir courbe A = f(t) en annexe) :
A = ε470××[I2] avec une mesure au maximum d’absorption du diiode (λ = 470 nm) pour une meilleure précision.
 Masse de diiode : À partir d’un tableau d’avancement, on peut dire que n(I2) = no – x ou x = no – n(I2)
D’après la courbe x = f(t), on détermine la valeur de l’avancement maximal xmax = 0,080 mmol. Or, xmax = no – 0
car le diiode est le réactif limitant (il est indiqué qu’il reste du zinc solide à la fin de la réaction). On peut en
déduire la valeur initiale de diiode dans la solution S : no = 0,080 mmol
Il y a donc 0,080 mmol de diiode dans 2 mL de solution commerciale, soit la quantité n = 50 × 0,080 = 4,0 mmol
dans 100 mL.
Puis, la masse de diiode m = n×M ; A.N. : m = 4.10-3×254 = 1,0 g pour 100 mL de solution commerciale.
On retrouve bien la valeur donnée dans le texte (doc.1) soit 1%.
Remarque : On peut aussi utiliser l’absorbance initiale : A0 = ε470××[I2]o soit [I2]o = A0 / (ε470×)
A.N.: [I2]0 = 1,20
(1,5.103  1,0) = 0,80 mmol.L-1 soit 50  0,080 = 40 mmol.L-1 dans la solution mère.
Dans 100 mL de solution S, il y a 40  0,100 = 4,0 mmol de diiode.
 Cinétique : La réaction du diiode avec le zinc est lente (durée de fin de réaction tR = 2500 s). On détermine le temps
de demi-réaction t1/2 pour x = xmax
2 = 0,080 2 = 0,040 mmol. Soit t1/2 = 150 s.
On remarque que cette durée est supérieure à celle de la seconde expérience (éclairage lumineux). On peut donc en
conclure que l’éclairement accélère la réaction (comme l’indique le doc.1) sans être pour autant un catalyseur (un
photon n’est pas une espèce chimique).
 Conclusion : La solution commerciale possède 1% de diiode et son efficacité est réduite au contact de certains
métaux (ici le zinc) et en présence de lumière.

13/12/2014 Devoir_commun2013_1_corr.doc 4/4
I
1.1
1
2
/28
1.2
1
2
1.3
1
1.4
1
2
3
CS-U
2.1
1
2.2
1
2.3
1
2.4
1
2
3.1
1
2
3
CS-U
3.2
1
2
3.3
1
3.4
1
2
3
3.5
1
4.1
1
2
4.2
1
4.3
1
2
II
1.a
1
/32
1.b
1
2
2.a
1
2
3
CS-U
2.b
1
2
CS-U
2.c
1
2
CS-U
3.a
1
3.b
1
2
CS-U
4.a
1
2
3
4
4.b
1
2
5.a
1
2
5.b
1
5.c
1
2
6.a
1
2
6.b
1
2
CS-U
6.c
1
2
CS-U
6.d
1
2
III
problématique
1
2
/20
équation-bilan
1
2
utilisation courbe A=f(t)
1
2
3
4
5
calcul de m(I2)
1
2
3
4
5
CS-U
cinétique de la réaction
1
2
3
4
conclusion
1
2
TOTAL : ............/80
NOTE : ............/20