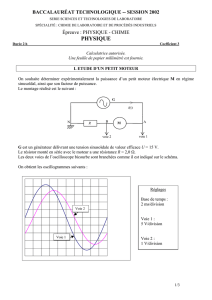
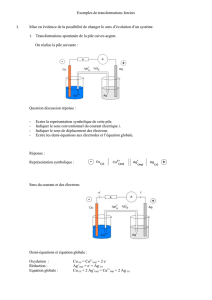
Transparents de la présentation.

Analyse mathématique du modèle
Analyse mathématique du modèle
d'électrodéposition de l'alliage Nickel-Fer
d'électrodéposition de l'alliage Nickel-Fer
sur une électrode tournante à disque
sur une électrode tournante à disque
NouEddine Alaa

Plan
Plan
I
I Modélisation du problème Modélisation du problème
II Analyse mathématique du modèle
II Analyse mathématique du modèle
III Extensions et Problèmes ouverts
III Extensions et Problèmes ouverts

Introduction
Introduction
Le principe de L'électrodéposition des alliages est
Le principe de L'électrodéposition des alliages est
très simple: c
très simple: c’ ’est une électrolyse. Il s est une électrolyse. Il s’ ’agit de agit de
réactions déclenchées par une source de courant.
réactions déclenchées par une source de courant.
Cathode: l Cathode: l’ ’objet qui doit subir le traitement objet qui doit subir le traitement
 Anode: métal avec lequel on traite la cathode Anode: métal avec lequel on traite la cathode
 Bain d Bain d’é ’électrolyse: l lectrolyse: l’é ’élément critique de la cellule lément critique de la cellule

 les films d'alliages de les films d'alliages de NiFe NiFe ont ont
largement été adoptés dans l'industrie
largement été adoptés dans l'industrie
électronique : enregistrement, mémoire
électronique : enregistrement, mémoire
et dispositifs de stockage.
et dispositifs de stockage.
 L'électrodéposition de l'alliage L'électrodéposition de l'alliage NiFe NiFe
est anormale: le métal le moins noble se
est anormale: le métal le moins noble se
dépose préférentiellement.
dépose préférentiellement.

•
• Talbot, Tobias Talbot, Tobias Ramasubramanian Ramasubramanian (1993) la (1993) la
codéposition
codéposition anormale de anormale de NiFe NiFe se produit car se produit car
apparition près de la cathode de
apparition près de la cathode de FeOH FeOH+
+ avec
avec
des concentrations supérieures à
des concentrations supérieures à NiOH NiOH+
+
•
• Matlosz Matlosz, , Pritzker Pritzker (1996) proposent un (1996) proposent un
modèle de transport stationnaire plus probant
modèle de transport stationnaire plus probant
sans tenir compte de la présence de
sans tenir compte de la présence de FeOH FeOH+
+
et de
et de NiOH NiOH+
+