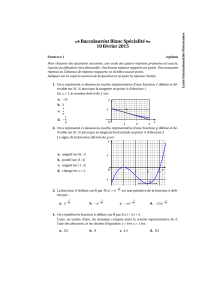
Correction Bac Blanc - 10 février 2015

Lycée International des Pontonniers
[Baccalauréat Blanc \
10 février 2015 – Corrigé
Exercice 1 4 points
Commun à tous les candidats
1. Réponse d. :−1
e
Le coefficient directeur de la tangente est négatif et n’est manifestement pas −2e ≈ −5,4.
2. Réponse b. : positif sur [3; 4]
En effet la fonction gest croissante sur cet intervalle.
3. Réponse c. :−xe−x2
2
On calcule H′(x) en appliquant la formule eu(x)′ =u′(x)eu(x).
4. Réponse a. : 6,5
k(0) =5 et k(1) =8 ; de plus la fonction kest représentée par une droite. On cherche donc l’aire
d’un trapèze de petite base 5, de grande base 8 et de hauteur 1.
Exercice 2 5 points
Commun à tous les candidats
Une personne décide d’ouvrir un compte épargne le premier janvier 2014 et d’y placer 2 000 euros. Le
placement à intérêts composés est au taux annuel de 3 %. Elle verse 150 euros sur ce compte tous les
1er janvier suivants. Pour tout entier naturel n, on note unle montant présent sur ce compte au premier
janvier de l’année 2014+naprès le versement de 150 euros. On a u0=2000.
Partie A
1. Les intérêts la première année sont de : 2000 ×3
100 =60 ; on a donc au bout d’un an : 2000+60 +
150 =2210. Donc u1=2210.
Les intérêts la deuxième année sont de : 2210 ×3
100 =66,30 ; on a donc au bout de deux ans :
2210+66,30+150 =2426,30. Donc u2=2426,30.
2. Ajouter 3 % à un nombre, c’est multiplier par 1+3
100 =1,03.
Pour passer de l’année nà l’année n+1, on multiplie le capital par 1,03 puis on ajoute 150 ; donc
un+1=1,03un+150, pour tout entier naturel n.
3. Pour tout entier n, on pose vn=un+5000 donc un=vn−5000.
vn+1=un+1+5000 =1,03un+150+5000 =1,03(vn−5000)+5150 =1,03vn−5150+5150 =1,05vn
v0=u0+5000 =2000 +5000 =7000
Donc la suite (vn) est géométrique de raison q=1,03 et de premier terme v0=7000.
4. La suite (vn) est géométrique de raison q=1,03 et de premier terme v0=7000 donc, pour tout
entier n,vn=v0×qn=7000×1,03n.
Comme pour tout n,un=vn−5000, on déduit que pour tout n,un=7000×1,03n−5000.
5. Cette personne aura au moins 4000 euros sur son compte dès que un⩾4000.
1ère méthode : On peut également calculer u3,u4... u8et u9, puis signaler que
u8=3867,39 <4000 et que u9=4133,41 >4000.

Baccalauréat ES Lycée International des Pontonniers
2ème méthode : utiliser un programme :
Variables : N est un nombre entier
Initialisation : Affecter à N la valeur 0
Traitement : Tant que 7000×1,03N−5000 <4000 Faire
Affecter à Nla valeur N+1
Fin du Tant que
Sortie : Afficher N
4ème méthode : représenter graphiquement les fonctions fet gdéfinies par :
f(x)=7000×1,03x−5000 et g(x)=4000 et rechercher l’abscisse du point d’intersection des deux
courbes représentatives de Cfet Cg.
5ème méthode : On résout l’inéquation
un⩾4000 ⇐⇒ 7000×1,03n−5000 ⩾4000
⇐⇒ 7000×1,03n⩾9000
⇐⇒ 1,03n⩾9000
7000
⇐⇒ ln1,03n⩾ln 9
7croissance de la fonction ln sur ]0; +∞[
⇐⇒ n×ln1,03 ⩾ln 9
7propriété de la fonction ln
⇐⇒ n⩾
ln 9
7
ln1,03 car ln1,03 >0
Or
ln 9
7
ln1,03 ≈8,5 donc c’est à partir de n=9 que la personne aura au moins 4 000 euros sur son
compte, c’est-à-dire à partir de l’année 2014+9=2023.
Partie B
L’algorithme ci-dessous modélise l’évolution d’un autre compte épargne, ouvert le premier janvier 2014,
par une seconde personne.
Variables : C et D sont des nombres réels
N est un nombre entier
Entrée : Saisir une valeur pour C
Traitement : Affecter à N la valeur 0
Affecter à D la valeur 2×C
Tant que C <D faire
affecter à C la valeur 1,03×C+600
affecter à N la valeur N +1
Fin du Tant que
Sortie : Afficher N
1. a. Dans cet algorithme, la variable C représente la somme que possède la personne l’année
2014+N.
b. On sait que C reçoit 1,03×C+600 donc le capital est multiplié par 1,03 ce qui correspond à
une augmentation de 3 %.
c. On sait que C reçoit 1,03 ×C+600 donc le versement annuel fait par cette personne est de
600 euros.
2. On saisit, pour la variable C, la valeur 3 000.
Bac Blanc – Corrigé 210 février 2015

Baccalauréat ES Lycée International des Pontonniers
a. Pour cette valeur de C, on complète le tableau en suivant pas à pas l’algorithme :
Valeur de C 3 000 3 690 4 400,70 5 132,72 5 886,70 6 663,30
Valeur de N 012345
Valeur de D 6 000 6 000 6 000 6 000 6 000 6 000
Test C <Dvrai vrai vrai vrai vrai faux
b. L’algorithme affiche la valeur de N en sortie de boucle, c’est-à-dire dès que C devient supérieur
ou égal à D ; l’algorithme affiche donc 5.
La variable D est égale au double du capital initial ; cet algorithme donne donc le nombre
d’années qu’il faut pour que le capital double, donc 5.
À partir de 2014+5=2019, le capital aura doublé.
Exercice 3 5 points
Enseignement obligatoire
1. Déterminer : P(A), P(T), P(V), PA(V) et PT(V).
D’après les données de l’énoncé :
•40% des clients utilisent la compagnie pour des raisons professionnelles alors, P(A)=0,4
•35% des clients utilisent la compagnie pour des raisons touristiques alors, P(T)=0,35.
•Sur l’ensemble de la clientèle, 40% choisit de voyager en première classe alors, P(V)=0,4.
•60% des clients pour raisons professionnelles voyagent en première classe alors, PA(V)=0,6.
•20% des clients pour raison touristiques voyagent en première classe alors, PT(V)=0,2.
On peut représenter la situation à l’aide d’un arbre.
Ω
A
0,4
V
0,6
V
T
0,35 V
0,2
V
D
V
V
2. a. Déterminer la probabilité que le client interrogé voyage en première classe et pour des raisons
professionnelles.
P(V∩A)=PA(V)×P(A)
=0,6×0,4
=0,24
La probabilité que le client interrogé voyage en première classe et pour des raisons profes-
sionnelles est égale à 0,24.
b. Déterminer la probabilité que le client interrogé voyage en première classe et pour des raisons
touristiques.
P(V∩T)=PT(V)×P(T)
=0,2×0,35
=0,07
La probabilité que le client interrogé voyage en première classe et pour des raisons touris-
tiques est égale à 0,07.
Bac Blanc – Corrigé 310 février 2015

Baccalauréat ES Lycée International des Pontonniers
c. En déduire la probabilité que le client interrogé voyage en première classe et pour des raisons
autres que professionnelles ou touristiques.
A,Tet Dforment une partition de l’univers Ωalors, d’après la formule des probabilités to-
tales :
P(V)=P(V∩A)+P(V∩T)+P(V∩D)
D’où
P(V∩D)=P(V)−P(V∩A)−P(V∩T)
=0,4−0,24−0,07
=0,09
3. Déterminer la probabilité que le client interrogé voyage pour des raisons professionnelles sachant
qu’il a choisi la première classe.
PV(A)=
P(V∩A)
p(V)
=0,24
0,4
=0,6
La probabilité que le client interrogé voyage pour des raisons professionnelles sachant qu’il a
choisi la première classe est égale à 0,6.
4. a. Chaque client a deux possibilités : soit il voyage en première classe avec une probabilité de
p=P(V)=0,4, soit non.
Nous sommes donc dans le cas d’une épreuve de Bernoulli que l’on répète 50 fois de manière
identique et indépendante, c’est donc un schéma de Bernoulli de paramètres n=50, p=0,4.
La variable aléatoire Xest la variable aléatoire comptant le nombre de succès de cette épreuve,
Xsuit donc une loi binomiale B(n,p) de paramètres n=50, p=0,4.
b. avec la calculatrice on trouve P(X=20) ≈0,11
EXERCICE 3 5 points
Candidats ayant suivi l’enseignement de spécialité
A B
C
D
E
1. sommets A
⃝B ⃝C ⃝D ⃝E ⃝
degré 3 4 2 2 3
Comme le graphe est connexe (exemple ABC E AD est une chaîne reliant tous les sommets) et
comme il y a exactement deux sommets de degré impair A ⃝et E ⃝, il y a une chaine eulérienne qui
commence et finit par chacun de ces deux sommets, et comme la somme des degrés est 14, il y a
7 arêtes.
A,B,D,A,E,C,B,Eest un tel itinéraire complet d’accrobranches, empruntant une fois et une seule
chaque parcours et commençant par l’arbre numéro A.
Bac Blanc – Corrigé 410 février 2015

Baccalauréat ES Lycée International des Pontonniers
2. a. La matrice M:
M=
01011
10111
01001
11000
11100
.
b. On utilise la matrice M3, et son coefficient situé en première ligne quatrième colonne m(
143).
C’est 5 ; c’est le nombre d’« itinéraires express » qui débutent à l’arbre numéro A, empruntent
trois parcours d’accrobranches et finissent à l’arbre D. Ce sont
A, E , B , D ;
A ,B ,A , D ;
A, E , A , D ;
A ,D , A , D ;
A , D , B , D .
3. a. •On sait que K(20 ; 0) est sur la courbe Cdonc f(xK)=yKdonc
f(20) =0 or f(20) =a×202+b×20+c
donc 400a+20b+c=0, c’est la première ligne du système.
•On sait que J(10 ; 2,5) est sur la courbe Cdonc f(xJ)=yJdonc
f(10) =2,5 or f(10) =a×102+b×10+c
donc 100a+10b+c=2,5, c’est la deuxième ligne du système .
•On sait que I(2 ; 8,1) est sur la courbe Cdonc f(xI)=yI
donc f(2) =8,1 or f(2) =a×22+b×2+c
donc 4a+2b+c=8,1, c’est la troisième ligne du système.
b. Prenons X=
a
b
c
et V=
0
2,5
8,1
alors le système précédent est équivalent à
U X =Voù U=
400 20 1
100 10 1
4 2 1
.
c. La calculatrice nous permet de savoir que U−1existe .
On sait qu’alors : U X =V⇐⇒ X=U−1V.
On trouve à la calculatrice que
U−1V=
1
40
−1
10
Ainsi, a=1
40,b= −1 et c=10. Donc f(x)=1 40 x2−x+10
EXERCICE 4 6 points
Commun à tous les candidats
On considère fla fonction définie sur Rpar f(x)=xe−x+1.
On note Cfla courbe représentative de la fonction fdans un repère orthonormé du plan et f′la fonc-
tion dérivée de f.
1. a. f′(x)=1×e−x+x×(−1)e−x=e−x(1−x)
b. Pour tout réel x, e−x>0 ; donc f′(x)est du signe de 1−x.
Bac Blanc – Corrigé 510 février 2015