EXERCICES : Lois à densité : Loi exponentielle. Définition : Une

EXERCICES : Lois à densité : Loi exponentielle.
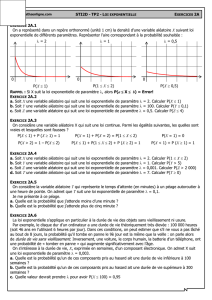
Définition : Une variable aléatoire à valeurs dans [ 0 ; + ∞ [
suit la loi exponentielle de paramètre  si :
p(  ≤ T ≤  ) = 
.
La fonction f définie sur [ 0 ; + ∞ [ par f(x)= est appelée
fonction de densité de paramètre .
Propriété :
Si une variable aléatoire T suit la loi exponentielle de paramètre  alors :
Pour tout t ≥ 0, on a : p ( T ≤ t ) = 1 –  .
Et son espérance E(T)= 
 . ( L’espérance s’interprète comme une moyenne )
Exercice 1 : Utilisation de la loi exponentielle.
1. La durée de vie, en heures, d’une diode est une variable aléatoire T qui suit la loi
exponentielle de paramètre 0,0008 ; déterminer la probabilité que :
a. La diode tombe en panne avant 4 000 h.
b. Fonctionne sans panne au moins 5000 h.
c. Tombe en panne entre la 4000 ° et la 5000 ° heure.
2. Pour un autre type de diode, la durée de fonctionnement, en heures, est une variable
aléatoire T’ qui suit une loi exponentielle. La durée de vie moyenne de ce type de diode est
1600 heures. Déterminer le paramètre de la loi T’.
Exercice 2 : La durée de vie, en heure, d’un composant électronique est une variable aléatoire T qui
suit la loi exponentielle de paramètre 0,00005. Déterminer la probabilité que le composant
électronique :
1.
a. tombe en panne avant 10 000 h.
b. Fonctionne sans panne au moins 15 000 h
c. Tombe en panne entre la 10 000° et la 15 000° heure. Donner la valeur exacte
puis la valeur arrondie à 10 –3 près.
2. Calculer l’espérance de T et en donner une interprétation.
Exercice 3 : Soit T une variable aléatoire qui suit la loi exponentielle de paramètre 0,02.
Déterminer les probabilités suivantes : a) p ( T ≤ 50 ) ; b) p( T > 100 ) ; c) p(T=200) .
Exercice 4 : Une agence de voyages a ouvert un guichet dans un centre commercial. On admet que le
temps T en minutes de passage d’un client à ce guichet suit une loi exponentielle de paramètre
=0,1. Vous arrivez à l’agence au moment où un client se présente au guichet, il n’y a pas d’autres
clients qui attendent. Dans tout l’exercice, déterminer la valeur exacte puis la valeur arrondie à 10–2
près du résultat.
Calculer la probabilité que votre temps d’attente soit :
a) De moins de 5 minutes.
b) De plus de 5 minutes.
c) Entre 5 et 15 minutes.

EXERCICES : Lois à densité : Loi exponentielle.
Définition : Une variable aléatoire à valeurs dans [ 0 ; + ∞ [
suit la loi exponentielle de paramètre  si :
p(  ≤ T ≤  ) = 
.
La fonction f définie sur [ 0 ; + ∞ [ par f(x)= est appelée
fonction de densité de paramètre .
Propriété :
Si une variable aléatoire T suit la loi exponentielle de paramètre  alors :
Pour tout t ≥ 0, on a : p ( T ≤ t ) = 1 –  .
Et son espérance E(T)= 
 . ( L’espérance s’interprète comme une moyenne )
Exercice 1 : Utilisation de la loi exponentielle.
1. La durée de vie, en heures, d’une diode est une variable aléatoire T qui suit la loi
exponentielle de paramètre 0,0008 ; déterminer la probabilité que :
a. La diode tombe en panne avant 4 000 h.
b. Fonctionne sans panne au moins 5000 h.
c. Tombe en panne entre la 4000 ° et la 5000 ° heure.
2. Pour un autre type de diode, la durée de fonctionnement, en heures, est une variable
aléatoire T’ qui suit une loi exponentielle. La durée de vie moyenne de ce type de diode est
1600 heures. Déterminer le paramètre de la loi T’.
Exercice 2 : La durée de vie, en heure, d’un composant électronique est une variable aléatoire T qui
suit la loi exponentielle de paramètre 0,00005. Déterminer la probabilité que le composant
électronique :
1.
a. tombe en panne avant 10 000 h.
b. Fonctionne sans panne au moins 15 000 h
c. Tombe en panne entre la 10 000° et la 15 000° heure. Donner la valeur exacte
puis la valeur arrondie à 10 –3 près.
2. Calculer l’espérance de T et en donner une interprétation.
Exercice 3 : Soit T une variable aléatoire qui suit la loi exponentielle de paramètre 0,02.
Déterminer les probabilités suivantes : a) p ( T ≤ 50 ) ; b) p( T > 100 ) ; c) p(T=200) .
Exercice 4 : Une agence de voyages a ouvert un guichet dans un centre commercial. On admet que le
temps T en minutes de passage d’un client à ce guichet suit une loi exponentielle de paramètre
=0,1. Vous arrivez à l’agence au moment où un client se présente au guichet, il n’y a pas d’autres
clients qui attendent. Dans tout l’exercice, déterminer la valeur exacte puis la valeur arrondie à 10–2
près du résultat.
Calculer la probabilité que votre temps d’attente soit :
a) De moins de 5 minutes.
b) De plus de 5 minutes.
c) Entre 5 et 15 minutes.