Vecteurs et repérage dans l`espace

Vecteurs et repérage dans l'espace 1/3
VECTEURS ET REPERAGE DANS L’ESPACE
I) Vecteurs de l'espace
1) Extension de la notion de vecteur
• L'égalité
ABCD
=
uuuruuur
signifie que ABDC est un parallélogramme.
• Relation de Chasles : Pour tous points A, B et C de l’espace,
ACABBC
=+
uuuruuuruuur
.
• la longueur ou norme du vecteur
AB
uuur
se note
AB
uuur
et est égale à la distance AB.
2) Opérations sur les vecteurs
L'addition de deux vecteurs et la multiplication d'un vecteur par un réel se définissent comme pour les vecteurs du plan.
Ces deux opérations possèdent les mêmes propriétés qu'en géométrie plane.
II) Vecteurs colinéaires, vecteurs coplanaires
1) Vecteurs colinéaires
Définition : Deux vecteurs de l’espace
u
r
et
v
r
sont colinéaires s’il existe deux nombres réels a et b tels que
(a ;b) ' (0 ;0) et
0
uv
α+β=
r
rr
.
Remarque : Si
u
r
et
v
r
sont colinéaires, alors on peut écrire l’un en fonction de l’autre sous la forme
ukv
=
rr
où k est un
nombre réel.
Théorème :
• Les points A, B et C sont alignés , les vecteurs
AB
uuur
et
AC
uuur
sont colinéaires.
• Les droites (AB) et (CD) sont parallèles , les vecteurs
AB
uuur
et
CD
uuur
sont colinéaires.
2) Vecteurs coplanaires
Définition : Trois vecteurs de l’espace
u
r
,
v
r
et
w
r
sont coplanaires s’il existe trois nombres réels a, b et c tels que
(a ; b ; c) ' (0 ; 0 ; 0) et
0
uvw
α+β+γ=
r
rrr
.
Remarque : Si
u
r
,
v
r
et
w
r
sont coplanaires alors on peut écrire l’un des trois en fonction des deux autres sous la forme
ukvkw
′
=+
rrr
où k et k’ sont des nombres réels.
Théorème :
• Les points A, B, C et D sont coplanaires , les vecteurs
AB
uuur
,
AC
uuur
et
AD
uuur
sont coplanaires.
• La droite (ED) est parallèle au plan (ABC) , les vecteurs
AB
uuur
,
AC
uuur
et
ED
uuur
sont coplanaires.
III) Repères et coordonnées dans l’espace
1) Repères de l’espace
Définition : Soit O un point de l’espace. On dit que
(,,,)
Oijk
r
rr
est un repère de l’espace, lorsque les vecteurs
i
r
,
j
r
et
k
r
ne sont pas coplanaires.

Vecteurs et repérage dans l'espace 2/3
Définition : Soit
(,,,)
Oijk
r
rr
un repère de l’espace.
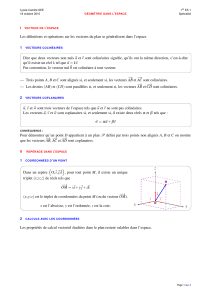
• Pour tout point M, il existe trois nombres réels
x, y et z tels que : OMxyz
ijk
=++
uuuur
r
rr
;
(x ; y ; z) sont les coordonnées de M dans le repère
(,,,)
Oijk
r
rr
.
x est l’abscisse, y l’ordonnée et z la cote du point M dans ce repère.
• Tout vecteur
u
r
de l’espace peut s'écrire :
xyz
uijk
=++
r
rr
r
; (x ; y ; z) sont les coordonnées de
u
r
.
O
m'(x ; 0 ; 0) M''(x ; y ; 0)
m''(0 ; y ; 0)
M'(x ; 0 ; z)
m'''(0 ; 0 ; z)
M(x ; y ; z)
M'''(0 ; y ; z)
i
r
y
j
r
j
r
x i
r
k
r
z k
r
kji
r
r
r
zyx
+
+
2) Propriétés : On considère un repère orthonormé
(,,,)
Oijk
r
rr
de l’espace.
Propriétés :
• Soit
u
r
(x ; y ; z) et
v
r
(x’ ; y’ ; z’).
•
0xyz0
u
=⇔===
r
r
; •
xx'
yy'
zz'
uv
=
=⇔=
=
rr ;
•
u
r
+
v
r
a pour coordonnées (x + x’ ; y + y’ ; z + z’) ;
• k
u
r
a pour coordonnées (kx ; ky ; kz).
‚ Soit A (xA ; yA ; zA) et B (xB ; yB ; zB).
•
AB
uuur
a pour coordonnées (xB − xA ; yB − yA ; zB − zA).
• Le milieu du segment [AB] a pour coordonnées ABABAB
xxyyzz
;;
222
+++
.
• Si de plus, le repère est orthonormé, on a :
222
()()()
BABABA
ABABxxyyzz
==−+−+−
uuur
.
IV) Equations d’objets de l’espace
1) Plans parallèles aux plans de base
Théorème :
• Tout plan parallèle au plan (O,
i
r
,
j
r
) d’équation z = 0 a une équation du type z = z0.
• Tout plan parallèle au plan (O,
j
r
,
k
r
) d’équation x = 0 a une équation du type x = x0.
• Tout plan parallèle au plan (O,
i
r
,
k
r
) d’équation y = 0 a une équation du type y = y0.
2) Sphère centrée sur l’origine O
Théorème : la sphère de centre O et de rayon R a pour équation
2222
xyzR
++=
.

Vecteurs et repérage dans l'espace 3/3
3) Cylindres
Théorème : Le cylindre de révolution d’axe (O,
k
r
), compris entre les plans d’équations z = a et z = b et dont les bases
sont des cercles de rayon R est défini analytiquement par le système
222
azb
xyR
≤≤
+=
.
Remarques :
• On peut aussi s’intéresser au cylindre illimité dont l’équation est
222
xyR
+=
.
‚ Pour les deux autres axes, on obtient des équations de cylindre analogues :
• cylindre d’axe (O,
i
r
) :
222
yzR
+= • cylindre d’axe (O,
j
r
) :
222
xzR
+=.
4) Cônes
Théorème : Le cône de révolution, de sommet O, d’axe (O,
k
r
), de hauteur h et dont le cercle de base a pour rayon R est
défini par le système 2
222
0zh
R
xyz
H
≤≤
+=
.
Remarques :
• On peut s’intéresser à la surface illimitée d’équation 2
222
R
xyz
H
+= qu’on appellera bi-cône, le rapport
R
h
donnant la tangente du demi-angle au sommet.
‚ Pour les deux autres axes, on obtient des équations de cône analogues :
• cône d’axe (O,
i
r
) : 2
222
R
yzx
h
+=
 • cône d’axe (O,
j
r
) : 2
222
R
xzy
h
+=
 .