Cours sur la trigonométrie Première Pro - Maths

http://maths-sciences.fr Première Pro
Cours sur la trigonométrie 1/2
T
TR RI IG GO ON NO OM MÉ ÉT TR RI IE E
I) Mesure d’un angle en radians
Les mesures d’angle peuvent être exprimées en degrés ou en radians.
 1 rad 57,30 °.
 Un angle plat a pour mesure radians ou 180 °.
 Les mesures d’angles en radians sont proportionnelles aux mesures en degrés.
en degrés
0
30
45
60
90
en radians
0
6
4
3
2
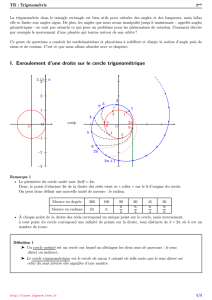
II) Cercle trigonométrique
Soit un repère orthonormal
O;OA;OB
. Le cercle trigonométrique est le cercle de rayon 1
centré sur l’origine du repère.
1R OA OB  
.
Sur ce cercle, le sens positif de rotation est le sens inverse des aiguilles d’une montre ou sens
trigonométrique.
A et M sont deux points du cercle trigonométrique. L’angle orienté des vecteurs
OA
et
OM
,
noté
OA, OM
, est l’amplitude de la rotation de centre O qui amène le point A sur le point
M.
Remarques
 Un angle orienté admet une infinité de mesures dépendant des nombres de tours effectués
« pour aller de A à M ».
 La mesure principale de l’angle orienté
OA, OM
est celle qui appartiendra à l’intervalle
;
.
 L’angle
OA, OM
ayant pour mesure principale exprimée en radians, les autres
mesures sont de la forme : α + 2kπ où k est un nombre réel
B
M
O A

http://maths-sciences.fr Première Pro
Cours sur la trigonométrie 2/2
III) Sinus et cosinus d’un nombre réel
Soit le cercle trigonométrique associé au repère orthonormal
O;OA;OB
.
est un nombre réel et M un point du cercle tel que
OA, OM
= .
 Le cosinus de , noté cos , est l’abscisse du point M.
 Le sinus de , noté sin , est l’ordonnée du point M.
en degrés
0
30
45
60
90
en radians
0
6
4
3
2
cos
1
3
2
2
2
1
2
0
sin
0
1
2
2
2
3
2
1
Propriétés
étant quelconque :
-1 cos 1
-1 sin 1
22
cos sin 1
 La tangente du nombre réel tel que
cos 0
est le réel :
sin
tan cos
B
sin
M
O cos
A
0
1
1
30°
45°
60°
1
2
2
2
3
2
2
2
1
2