La fonction carrée est une fonction paire

La fonction carrée est une
fonction paire

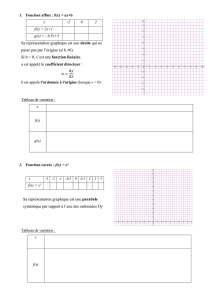
Intéressons nous à la courbe
représentative de la fonction carrée,
que l’on appellera dans la suite f.

o
-2 2
2
4
i
j
I
J
Oa
Mf(a)
Soit M un point de Cf
Si a est l’abscisse de M, alors
f(a)=a² est son ordonnée.

Ce point symbolise la transformation
de a en f(a)=a² par la fonction f
(fonction carrée).
o
-2 2
2
4
i
j
I
J
Oa
Mf(a)

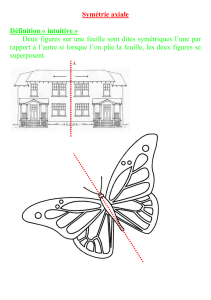
Soit N le symétrique de M par rapport à
l’axe des ordonnées (Oy).
o
-2 2
2
4
i
j
I
J
Oa
Mf(a)
-a
N