CORRECTION

CORRECTION BREVET 2014 AMÉRIQUE DU NORD
Exercice 1:
1) Réponse B : 
2) Réponse B : Calculons ce pgcd par l’algorithme d’Euclide :
133 = 841 + 49
84 = 49×1 + 35
49 = 35×1 + 14
35 = 14×2 + 7
14 = 7×2 + 0 Le PGCD est le dernier reste non nul donc PGCD (134 ; 84) = 1.
3) Réponse A : −3x+5  9  −3x  9−5  −3x > 4 
é
4) Réponse C : (1+)2 = 1+2+2 = 3+2
Exercice 2 : Le boudin est constitué d’une sphère de diamètre 16 cm donc de rayon 8 cm et d’un cylindre de révolution
de même rayon et de hauteur 50 cm :
Vboule = 
 cm3.
Vcylindre =  r² h = ×8²×50 = 3 200 cm3.
D’où Vboudin =
 cm3 ≈ 12 197,76 cm3.
Exercice 3 :
1) 240  8 = 30 h. Il faut 30 h pour effectuer ce trajet sans faire de pause.
2) Vécluse = 30 ×8,4 ×3 = 756 cm3.
3) 882  
 = 882×1,27 = 1 120,14 €. Le prix pour cette période est de 1 120,14 €.
Exercice 4 :
1. Il faut saisir B3+C3+D3+E3+F3+G3+H3+I3+J3+K3+L3 ou SOMME(B3 : L3).
2. Quand on ajoute les valeurs du tableau on obtient −21,47.
3. Le parcours est donc descendant.
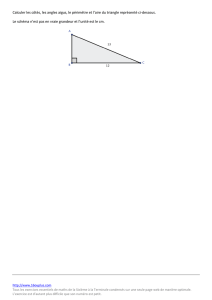
Exercice 5 : D’après le théorème de Pythagore dans le triangle ACE rectangle en C :
CA2+CE2 = AE2 soit 342+CE2 = 562 d’où CE2 = 562−342 = 3 136−1 156 = 1 980
CE =  ≈ 44,5 cm CE > 0 c’est une longueur.
Comme 44 < 44,5 < 46, on en déduit que ce siège est donc parfaitement adapté.
Exercice 6 :
1) Le dé est équilibré donc la chance d’obtenir chaque face est la même.
2) Il y a 6 issues pour le dé rouge et 6 issues pour le dé jaune. Avec le principe multiplicatif, Cela représente
donc 6×6 = 36 issues.
3) Il manque 1 000 – 650 = 350 points. Pour gagner à son troisième lancer Paul doit donc obtenir l une
des 4 issues suivantes : une paire de 1, de 4, de 5 ou de 6.
La probabilité de gagner à son troisième lancer est donc de 
.

Exercice 7 :
1) v =    =                m.s-1.
2) On cherche x tel que v = 0 soit         ,
donc pour que la vitesse soit nulle il faut que 4,3 – x = 0  x = 4,3 m.
La vitesse d écoulement sera nulle pour x = 4,3 m, c’est-à-dire lorsque la hauteur de l’eau dans l’écluse est la même que
la hauteur de l’eau en amont.
3) La vitesse d écoulement est de 4,2 m.s-1.
Exercice 8 :
1) S =  r² = ×30² = 900 cm² = 0,09 m².
2) q = S v = 0,09×2,8 ≈ 0,792 m3.s-1.
3) Le résultat précédent indique que chaque seconde la vantelle laisse passer 0,792 m3d’eau.
Temps : 756 m3÷0,792 ≈ 954,5 s
954,5 = 15×60+54,5
Il faudra attendre 15 min 55s c’est un peu plus de 15 min.
Exercice 8 :
 Montrons que AH = 2,9 cm :
Le triangle APB est isocèle en P, donc la hauteur [PH] est aussi une médiane. Ainsi H est le milieu de [AB].
Donc AH = 5,8 2 = 2,9 cm.
 Calculons 
:  = 90° – 55° = 35°.
 Calculons AP : Dans le triangle APH rectangle en H, on a :
cos 
= 
 d’où cos 35° =   par suite AP =   ≈ 3,54 m.
Chaque porte mesure environ 3,54 m.