Sujet du bac pro spvl 2007

Nom :
Prénom :
Sujets d’examens : étude de
fonction
Classe :
Exercice 1 (bac pro SPVL 2007):
Pour contrer l'offensive du commerce sur Internet dans le domaine de la cosmétique, le salon SANTE-BEAUTE a
investi, depuis 4 ans, dans la publicité et l'aménagement de son point de vente.
Le responsable du salon a constaté que pour une somme investie s (exprimée en k€), le résultat R réalisé, vérifie
la formule R(s) = – 6s2 + 51s + 12.
1) Calculer le résultat pour une somme investie de 3 k€.
Le résultat est noté R(s) et la somme investie est notée s, on remplace donc s = 3 dans l’expression de R(s), on
obtient donc :
R(3) = - 6 × 32 + 51 × 3 + 12 = - 54 + 153 + 12 = 111
2) Soit la fonction f définie sur l'intervalle [1,5 ; 6] par : f(x) = –6x2 + 51x + 12
a) Compléter le tableau de valeurs de f sur l'annexe à rendre avec la copie.
On remplace chaque valeur de x dans l’expression de f(x).
x
1,5
2
2,5
3
3,5
4
4,5
5
5,5
6
y
75
90
102
111
117
120
120
117
111
102
b) Soit f ' la fonction dérivée de la fonction f sur l'intervalle [1,5 ; 6]. Calculer f '(x) et
Résoudre l'équation f '(x) = 0.
Calcul de f ‘(x)
f(x) = -6 × x2 + 51 × x + 12
f ’(x) = -6 × 2x + 51 × 1 + 0 = -12x + 51
Résoudre f ‘ (x) = 0 , c’est trouver la valeur de x qui annule f ‘(x) , on écrit donc :
f ‘(x) = 0
-12x +51 = 0
-12x = -51
x =
12
51
= 4,25
c) Compléter le tableau de variation de la fonction f sur l'annexe à rendre avec la copie.

1ère étape : Première chose à écrire dans le tableau : la valeur de x qui annule la dérivée. C'est-à-dire x = 4,25 et
un zéro sur la ligne du dessous.
2ème étape : Ensuite, on cherche le signe de la dérivée sur chaque intervalle du tableau. C'est-à-dire pour x compris
entre 1,5 et 4,25 et puis pour x compris entre 4,25 et 6
-Sur l’intervalle [1,5 ; 4,25], on prend une valeur de x au hasard que l’on remplace dans l’expression de la
dérivée.
Exemple : la valeur x = 2
On calcule alors f ‘(2) = -12 ×2 + 51 = -24 + 51 = 27 .C’est positif donc le signe de f ‘(x) sur l’intervalle [1,5 ;
4,25] sera positif et on met un « + » dans le tableau.
- Sur l’intervalle [4,25 ; 6], on prend une valeur de x au hasard que l’on remplace dans l’expression de la
dérivée.
Exemple : la valeur x = 5
On calcule alors f ‘(5) = -12 × 5 + 51 = -60 + 51 = -9 . C’est négatif donc le signe de f ‘ (x) sur l’intervalle
[4,25 ; 6] sera négatif et on met un «-» dans le tableau.
3ème étape : On met les flèches correspondantes au signe de la dérivée. (Rappel de cours, quand la dérivéeest
négative sur un intervalle alors la fonction est décroissante sur cet intervalle, quand elle est négative, la fonction
est croissante).
4ème étape : On calcule les valeurs de la fonction f au bout de chaque flèche.
Dans l’exercice : On doit donc calculer les valeurs de f(x) pour x =1,5 , x = 4,25 et x = 6
f(1,5) = -6 × 1,52 + 51 × 1,5 + 12 = 75
f(4,25) = -6 × 4,252 + 51 × 4,25 + 12
= 120,375
f(6) = -6 × 62 + 51 × 6 + 12 = 102
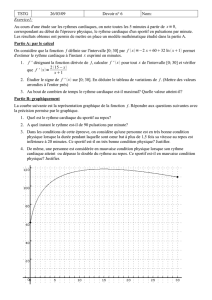
d) En utilisant le repère de l'annexe à
compléter et à rendre avec la copie,
représenter graphiquement la fonction f.
On n’oublie pas de rajouter à la courbe le
point qui annule la dérivée ! sinon on
trace une courbe qui n’est pas exacte.
e) Donner le maximum de la fonction f sur
[1,5 ; 6].
La fonction admet un maximum pour x =
4,25 (la valeur de x qui annule la dérivée) ,
et la valeur de ce maximum est f (4,25) =
120,375
3) En utilisant les réponses précédentes, donnez le montant de l'investissement (en euros) qui permet
d'obtenir un résultat maximum.
On revient au concret et dans le contexte du problème, on fait une phrase en français. Par exemple :
Le montant de l’investissement qui permet d’obtenir un résultat maximum est de 4,25 k€. Le résultat maximum
obtenu sera 120,375.