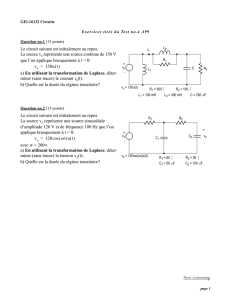
la transformée de Laplace - physique appliquée au LLA

BS 1 SE la transformée de Laplace
Lycée Louis Armand - MULHOUSE
Physique Appliquée - HASSENBOEHLER page 1 / 8
ou le calcul opérationnel
1. Intérêt de la transformée de Laplace
Les relations tension - courant des dipôles sont des relations intégro – différentielles.
Exemple du circuit RLC série :
u(t) = R . i(t) + L d i(t)
dt + 1 C ⌡
⌠
0
t i(t) dt (1)
dans le cas particulier des signaux purement sinusoïdaux, on utilise la notation
complexe pour les calculs de tensions et de courants.
C’est ce qu’on a appelé la transformée cissoïdale : C [ V 2 sin ( ω
ωω
ωt + ϕ
ϕϕ
ϕο
οο
ο )
]
= V. e jϕ
ϕϕ
ϕo
Les équations différentielles sont plus faciles à traiter ,
l’équation (1) se transforme en U (jω) = R . I (jω) + L . jω . I (jω) + 1
C . 1
jω . I (jω)
dans le cas d’un signal causal quelconque, ce sont les fonctions nulles aux temps négatifs,
on utilise la transformée de Laplace .
Les 2 applications les plus connues sont l’étude des régimes transitoires, l’étude des
systèmes asservis avec, en particulier, l’étude de la stabilité des fonctions de transferts, …
rappelons les autre transformée utiles en électronique :
la transformée de Fourier F ( s(t) ) = S ( f ) donnant le spectre d’un signal s(t)
la transformée en Z pour les signaux échantillonnés
2. Fonctions particulières : la fonction de Heaviside, l’impulsion de Dirac
Dans les régimes variables quelconques, on rencontre souvent des discontinuités. Pour les exprimer
mathématiquement, on introduit des fonctions discontinues de base :
la fonction de Heaviside et sa dérivée, l’impulsion de Dirac.
2.1. l’échelon unitaire ou fonction de Heaviside Γ
ΓΓ
Γ(t) Γ est la lettre grecque « gamma »
définition :
Γ(t) = 0 pour t < 0
Γ(t) = 1 pour t ≥ 0
l’image physique de ce signal est l’application d’une tension de 1 V
ou de 0 V par l’intermédiaire d’un inverseur K :
à t = 0 s, K passe de la position (2) à la position (1).
La fonction de Heaviside permet d’écrire les équations mathématiques
de signaux causaux et discontinus.
Pour cela on utilise la relation de translation dans le temps ou du retard :
si on retarde une fonction Γ
ΓΓ
Γ(t) d’une durée to, la fonction obtenue s’écrit Γ
ΓΓ
Γ(t - to)
C
L
i(t) R
u(t)
Γ(t – t
o
)
t
to
Γ
t
1
K
1 V
Γ
ΓΓ
Γ
(t)
(1)
(2)

BS 1 SE la transformée de Laplace
Lycée Louis Armand - MULHOUSE
Physique Appliquée - HASSENBOEHLER page 2 / 8
2.2. l’impulsion unité δ
δδ
δ ( t ) ou impulsion de Dirac
définition :
δ(t) = 0 pour t ≤ 0 et t ≥ ∆
δ(t) = 1
∆ pour t ∈ [0, ∆]
avec ∆ qui tend vers 0
on constate que l’aire de cette impulsion est égale à 1 : ⌡
⌠
-∞
+∞ δ ( t ) . dt = ⌡
⌠
0
∆ 1
∆ . dt = 1
L’impulsion de Dirac est unitaire car son aire ( et non son amplitude ) est égale à 1.
Si son aire vaut X (nombre réel ), on dit que le poids de l’impulsion de Dirac est de X.
Intérêt : elle est utilisée
pour définir les signaux échantillonnés : répétée infiniment à une fréquence fe = 1
Te ,
fe étant la fréquence d’échantillonnage et Te la période d’échantillonnage, on peut définir
le peigne de Dirac
∑
n = - ∞
+∞
δu( t - nTe ) , qui, multiplié par un signal s(t) produit le signal
échantillonné s*(t) = s(t) .
∑
n = - ∞
+∞
δu( t - nTe ) .
pour l’étude de la stabilité des systèmes asservis : une impulsion de Dirac appliquée à
un système produit à la sortie de ce système un signal égal à la fonction de transfert du
même système. Si la réponse à l’impulsion (ou réponse indicielle ou percussionnelle)
donne un signal ne tendant pas vers zéro, le système est instable.
3. La transformée de Laplace
À toute fonction réelle f(t) on associe une fonction
F(p)
de la variable complexe p :
F(p) = =⌡
⌠
0
00
0
+ ∞
∞∞
∞f(t) e-p t dt
Il est sous-entendu, puisque l’intégration de la fonction se fait de 0 à +∞,
que le signal transformé est le signal causal f(t). Γ(t).
On écrit L ( f(t) ) = F(p) en lisant “transformée de Laplace de f(t) est égale à F(p)”.
Vocabulaire : F(p) est l’image de f(t) : L ( f(t) ) = F(p)
et f(t) est l’original(e) de F(p) : L-1( F(p) ) = f(t)
p est la variable de Laplace ou variable symbolique
t
impulsion de DIRAC
δ(t)
δ
t
∆
1
∆
t
Té
peigne de Dirac
L
L
-1
F (p) f ( t )

BS 1 SE la transformée de Laplace
Lycée Louis Armand - MULHOUSE
Physique Appliquée - HASSENBOEHLER page 3 / 8
4. Propriétés remarquables de la transformée de Laplace : F(p) = =⌡
⌠
0
00
0
+ ∞
∞∞
∞f(t) e-p t dt
4.1. linéarité : L ( a . f1(t) + b . f2(t) ) = a . F1(p) + b . F2(p)
4.2. dérivation : L ( d f(t)
dt ) = p F(p) - f(0-) L ( d2 f(t)
dt2 ) = p2 F(p) - p f(0+) - d f(0-)
dt
si le signal est causal (conditions initiales nulles) : L
LL
L ( d f(t)
dt ) = p F(p)
4.3. intégration : L (
⌡
⌠
0
tf(t) dt ) = F(p)
p + 1 p g(0-) où g(t) =
⌡
⌠
0
t f(x)dx si le signal est causal : L
LL
L (
⌡
⌠
0
tf(t) dt ) = F(p)
p
4.4. retard : L
LL
L ( f(t - τ
ττ
τ) . Γ(
Γ(Γ(
Γ(t - τ
ττ
τ) ) = e -τ
ττ
τp . F(p) où τ est le retard
4.5. transformée d’une fonction amortie : L
LL
L ( e -at . f(t) ) = F(p + a)
4.6. changement de l’échelle des temps : L ( f ( t
a )) = a F(ap)
4.7. théorème de la valeur initiale et théorème de la valeur finale
théorème de la valeur initiale : lim
t→
→→
→0+ f ( t) = lim
p→
→→
→+∞
∞∞
∞ p. F ( p )
théorème de la valeur finale : lim
t→
→→
→+∞
∞∞
∞ f ( t) = lim p→
→→
→0 p . F ( p )
5. Transformées usuelles :
l’impulsion de Dirac : L
LL
L(δ
δδ
δ(t)) = 1 la fonction de Heaviside : L
LL
L(Γ
ΓΓ
Γ(t)) = 1
p
la rampe : L
LL
L(at) = a
p2 l’exponentielle : L
LL
L(e-at) = 1
p + a
le sinus : L(sin ωt) = ω
p2 + ω2 le cosinus : L(cos ωt) = p p2 + ω2
t à la puissance n-1 : L ( t(n-1)
(n-1)! ) = 1
pn
transformée F(p) d’un signal périodique f(t) de période T et dont la transformée
de la première onde est F1(p) : 1
p + a  F(p) = F1(p). 1
1 - e-pT
remarque : les relations ci dessus permettent de trouver l’originale f(t) = L -1( F(p) )
par exemple la fonction 3
p+2 a comme originale 3 e -2t,
sous entendu la fonction causale 3 e -2t Γ(t) représentée ci-contre :
0,5
3
t(s)
t
δ
t
Γ
t
a
at.Γ(t)
t
e-at.Γ(t)
t
f(t)
t
cos(ωt).Γ(t)
t
sin(ωt).Γ(t)

BS 1 SE la transformée de Laplace
Lycée Louis Armand - MULHOUSE
Physique Appliquée - HASSENBOEHLER page 4 / 8
6. La transformée inverse de Laplace ou l’originale
6.1. intérêt du calcul symbolique :
comme l’explique le diagramme ci-contre, l’intérêt
est de trouver la réponse s(t) d’un système
linéaire à un signal d’entrée e(t) causal.
On connaît l’équation différentielle du système, elle relie la grandeur de sortie s(t) à la grandeur
d’entrée e(t).
En régime harmonique le système est décrit par la fonction de transfert complexe T(jω), en
régime causal la transmit tance sera T(p).
La méthode pour retrouver l’originale consiste à transformer S(p) en somme d’expressions
connues dont on retrouve facilement les originales, grâce à la “table de Laplace” (§4 et §5).
6.2. Décomposition en éléments simples
Soit F(p) une fonction de la variable p qui peut s’écrire
F(p) = N(p)
D(p) = a + bp + cp2 + dp3 + … + kpm
a' + b' p + c'p2 + d'p3 + … + k'pn
où le numérateur N(p) est un polynôme en p de degré m et
où le dénominateur D(p) est un polynôme en p de degré n
avec n ≥
≥≥
≥ m puisqu’en physique la plupart des système existants sont des passe-bas.
Les racines du numérateur sont appelées les zéros de F(p)
Les racines du dénominateur sont appelées les pôles de F(p) ,
on peut alors mettre le dénominateur sous la forme suivante :
D(p) = (p - p1) (p - p2) (p - p3) … (p - pn) si p1, p2, p3 à pn sont les n pôles
et écrire F(p) = N(p)
(p - p1) (p - p2) (p - p3) … (p - pn) .
6.3. D(p) a n racines distinctes : on dit que les pôles sont simples
Dans ce cas on peut écrire :
F(p) = N(p)
(p - p1) (p - p2) (p - p3) … (p - pn) = A1 (p - p1) + A2 (p - p2) + …+ An (p - pn) .
Les résidus Ai sont facile à trouver.
En effet, il suffit, pour déterminer par exemple le résidu A2, de multiplier par (p - p2) les deux
quotients ci-dessus, ce qui donne
N(p) (p - p2)
(p - p1) (p - p2) (p - p3) … (p - pn) = A1 (p - p1) (p - p2)+ A2 (p - p2) (p - p2)+ …+ An (p - pn) (p - p2) .
système
T s(t)
e(t)
e(t)
résolution de
l’équation différentielle
S(p)
E(p)
T(p)
transmittance symbolique
calcul de
l’originale
calcul de
l’image
s(t)

BS 1 SE la transformée de Laplace
Lycée Louis Armand - MULHOUSE
Physique Appliquée - HASSENBOEHLER page 5 / 8
et après simplification N(p)
(p - p1) (p - p3) … (p - pn) = A1 (p - p1) (p - p2)+ A2 + …+ An (p - pn) (p - p2).
En remplaçant p par p2, tous les résidus Ai sauf A2 s’éliminent,
d’où A2 = N(p2)
(p2 - p1) (p2 - p3) … (p2 - pn)
De façon générale, à Ai = [ (p - pi) . F(p) ]p = pi .
Les résidus déterminés, l’originale sont des exponentielles , en effet L
LL
L-1(Ai
(p - pi) ) = Aiexp pit .
Exemple 1 : calculons les résidus A, B et C, pour en déduire l’originale f(t) :
F(p) = 2
(p - 1) (p + 2) p = A (p - 1) + B (p + 2) + C p
Exemple 2 : calculons les résidus A et B, pour en déduire l’originale f(t) :
F(p) = p + 1
p2 + 5 p + 6 = p + 1
(p + 2)(p + 3) = A (p + 2) + B (p + 3) =
6.4. D(p) a des racines doubles, multiples d’ordre k, …
Dans ce cas F(p) = N(p)
(p - po)k.D1(p) = Ak (p - po)k + Ak-1 (p - po)k-1 + …+ A1
(p - po) + N1(p) D1(p) .
Les résidus Ak peuvent être déterminés par différentes méthodes détaillées ci-dessous et le
rapport N1(p)
D1(p) avec les mêmes méthodes suivant que les pôles soient simples ou multiples.
Une formule générale pour les courageux : Ai = 1
i ! 
di [ ] (p - po)k F(p)
dpi p = po.