Le mouvement de rotation

1
Le mouvement de rotation
1. Activité
Un disque équipé d’un point rouge est relié à un moteur.
Rotation lente
Rotation rapide
Qu’observe-t-on si le moteur tourne lentement ?
Qu’observe-t-on si le moteur tourne rapidement ?
Quelle est la nature de la trajectoire du point rouge ?
Comment se situe le plan de la trajectoire par rapport à l’axe de rotation ?
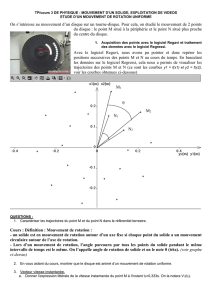
2. Expérience
Reprenons le disque monté sur son moteur. Le stroboscope éclaire le disque et indique la
fréquence de l’éclair (n éclairs par seconde).

2
Essayons de trouver la fréquence la plus ………………… qui nous permet de voir la marque au
même endroit.
La vitesse angulaire est l’angle, en radian, balayé par un rayon du solide en une seconde.
Un tour représente un angle de ……… ° soit ……… radian.
Si le disque effectue n tour en une seconde, la vitesse angulaire est donc égale à
…………………
En déduire la vitesse angulaire de notre disque :
Sur le disque tournant sont notés trois points A, B et C.
Complétez le tableau :
Point
A
B
C
Rayon R en m
OA=
OB=
OC=
Distance parcourue en 1
seconde en m
Vitesse v en m/s
Error! en rad/s
(vitesse angulaire)
Quel et le point qui a la plus grande vitesse linéaire ?
Pourquoi la vitesse angulaire est sensiblement la même pour les trois points ?
Quelle est la relation entre
Error!
et 2xπxn ?
3. Le mouvement de rotation
Un solide effectue un mouvement de rotation autour d’un axe si la trajectoire de chacun
de ses points est un cercle :
dont le centre est sur l’axe de rotation.
dont le plan est perpendiculaire à cet axe.
Pour un mouvement de rotation uniforme, chaque rayon décrit le même angle α pendant
une même durée t. La vitesse angulaire ω est définie par :
ω =
Error!
ω en rad/s α en radian t en s
Pour un mouvement de rotation uniforme la vitesse angulaire est constante.

3
La fréquence de rotation n représente le nombre de tours effectués par le solide en une
seconde.
A chaque tour, l’angle balayé est de 2xπ radian. Si le solide effectue n tours par seconde,
sa vitesse angulaire est :
ω = 2xπ x n
La vitesse linéaire d’un point du solide en rotation uniforme est la vitesse du point le long
de sa trajectoire :
v = ω x R
On déduit de la relation ω = 2xπ x n une autre expression de la vitesse :
v = 2xπ x n x R
soit
v = π x n x D