Mouvement de rotation et vitesse angulaire. T = Relation entre

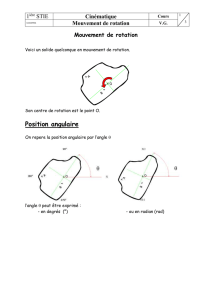
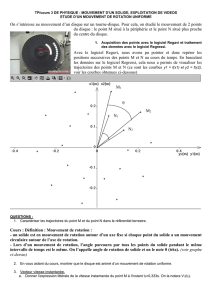
Mouvement de rotation et vitesse angulaire.
• L’angle θ décrit entre deux instants donnés est le même pour tous les
points du solide. On l’appelle l’angle de rotation du solide.
• Au cours d’une rotation, plus un point est éloigné de l’axe, plus la
longueur de l’arc décrit est grande : M 1 M 2 > P 1 P 2 car M plus loin de
l’axe que P.
Les points d’un solide en rotation n’ont pas la même vitesse.
En revanche, ils décrivent tous le même angle, il est donc intéressant de caractériser le
mouvement par la rapidité de la variation de cet angle.
Pour cela on utilise la notion de vitesse angulaire.
Pour avoir la vitesse angulaire instantanée, on procède comme pour une vitesse, on prend la
vitesse angulaire moyenne entre deux instants très proches.
Dans le cas d’un mouvement uniforme :
T
π
ω
2
= donc la période d’un mouvement circulaire est :
T =
ω
π
.2
Relation entre vitesse et vitesse angulaire.
En faisant un parallèle avec le fait que le périmètre d’un cercle se calcule par 2 π (angle : 360°) * r
(rayon du cercle) on trouve une relation entre l’angle et l’arc de cercle :
D’après la relation de la vitesse :

Exercice 1:
Un disque 45 tours à un diamètre d=17cm.
1. Calculer la fréquence du mouvement ainsi que la période.
2. Calculer la vitesse angulaire du disque.
3. Calculer la vitesse d'un point de la périphérie du disque et représenter le vecteur vitesse de ce
point.
Exercice 2:
1. Déterminer la vitesse angulaire de la grande aiguille d'une montre.
2. Déterminer la vitesse angulaire de la petite aiguille d'une montre.
3. On choisit l'origine des dates à midi. A quel instant les deux aiguilles se superposent-elles à
nouveau?
Exercice 3
Une scie circulaire d’un diamètre 60 cm tourne à 640 tours par minute.
1) Calculer sa fréquence de rotation, sa vitesse angulaire et la vitesse linéaire d’une de ses dents
(vitesse de coupe).
2) À quelle fréquence devrait tourner la scie pour que la vitesse de coupe soit de 30 m/s ?
Exercice 4
Un satellite géostationnaire tourne autour de la terre à la vitesse supposée constante de 11 000 km/h.
On suppose que sa trajectoire est une orbite circulaire de 42 000 km.
1) Calculer la vitesse angulaire de ce satellite.
2) Calculer la fréquence, puis la période de ce mouvement.
Expliquer l’appellation «géostationnaire».