CORRECTION EXERCICE3-MATH-EMMANUELLE

EXERCICE 3 :
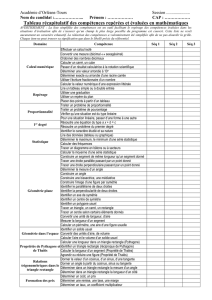
 Figure (elle n’est pas en vraie grandeur !)
 On applique le théorème de Pythagore dans le triangle FEL rectangle en E. On
a alors :
LE2 =FL2-FE2 (on cherche un petit côté).
Donc LE2 =102-82 =36 ; ce qui donne
cmLE 636 
.
EXERCICE 5 :
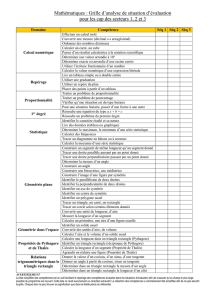
Données : FA = 18 m ; FE = 12,5 m et BE = 7,5 m.
NOTE : Tous les résultats seront arrondis au centième.
F
E
L
A
8 cm
10 cm
B
F
E
L
A

 Calcul de la distance FB.
On applique le théorème de Pythagore dans le triangle rectangle BEF rectangle
en B et qui donne :
FB2 = FE2-BE2 =12,52-7,52 =100. Donc FB =
100
=10 m.
 En déduire la distance LE.
On a LE =AB =FA-FB =18-10 =8m.
 Quelle est la nature du quadrilatère ALEB ? Justifier votre réponse.
Le quadrilatère ALEB est un rectangle car il a quatre angles droits ses côtés ne
sont pas tous de même longueur.
 Donner, en justifiant la réponse, la nature du quadrilatère FELA.
Le quadrilatère FELA est un trapèze car il a deux côtés parallèles ([FA] et [LE])
de longueurs différentes.
 Calculer l’aire 𝒜1 du quadrilatère FELA.
On a 𝒜1 =
2
5,97
25,7)818( 2)( m
BELEFA 
 Calculer l’aire 𝒜2 du demi-cercle de diamètre [LE].
Le rayon du demi-cercle est R=
m
LE 4
2
8
2
. On a alors :
𝒜2 =
2
22 12,25
2414;3 2m
R
 En déduire l’aire totale 𝒜 de l’institut.
On a 𝒜 =
2
62,12212,255,97 m
 Madame TOURTA décide de réserver l’espace circulaire à l’accueil. Quel
est alors le pourcentage de l’aire réservée à l’accueil par rapport à l’aire
totale de l’institut ?
On a le calcul
%5,20100
62,12212,25 
EXERCICE 7 :
On considère la figure ci-dessous formé d’un triangle LAC rectangle en A et
d’un demi-cercle.
Données : AL = 8 cm et AC = 6 cm (La figure n’est pas en vraie grandeur).
C
L
A

 Calculer l’aire 𝒜1 du triangle LAC.
On a 𝒜1 =
2
24
268 2m
ACAL 
 Calculer la longueur LC.
Le triangle ALC étant rectangle en A, l’affaire se règle par Pythagore et on a
vite :
LC2 = AL2 + AC2 =82 + 62 =100. Donc LC =
100
=10 m.
 Calculer l’aire 𝒜2 du demi-cercle de diamètre [LC].
Le rayon (moitié du diamètre) du demi-cercle est R=
m
LC 5
2
10
2
. On a alors :
𝒜2 =
2
22 25,39
2514;3 2m
R
 En déduire l’aire totale 𝒜 de la figure.
On a l’aire totale 𝒜 =
2
25,6325,3924 m
 Calculer le périmètre 𝓁 du demi-cercle.
On a directement 𝓁=
m
R7,15
2514;32 2
2
 En déduire le périmètre 𝑝 de la figure.
Le périmètre est la longueur totale que l’on parcourt en faisant un tour
complet sur le bord de la figure. On a donc :
𝑝 =AC + 𝓁 +LA=8+15,7+6=29,7m