CHAPITRE 7 SENS DE VARIATION D`UNE FONCTION I A partir d

CHAPITRE 7 SENS DE VARIATION D'UNE FONCTION
I A partir d'une situation géométrique
ABC est un triangle de hauteur [AH] tel que : AH = 3 cm, BH = 4 cm et
HC = 9 cm. M est un point du segment [BC]. On pose BM = x cm.
On considère la fonction f qui à x associe la distance AM.
La fonction f est définie sur l'intervalle [0;13].
La longueur du segment [AM] est minimale lorsque le point M est
confondu avec le point H. Cette longueur minimale est égale à 3 cm.
On dit: "3 est le minimum de la fonction f sur l'intervalle [0;13], il est
atteint pour x = 4."
Quand x varie de 0 à 4, la longueur AM diminue.
On dit que la fonction f est strictement décroissante sur l'intervalle [0;4].
Quand x varie de 4 à 13, la longueur AM augmente.
On dit que la fonction f est strictement croissante sur l'intervalle [4;13].
II A partir d'une courbe représentative
La fonction g est représentée par la courbe ci-dessous:
Page 1/3

La fonction g est définie sur l'intervalle [−6; 6].
La fonction g est strictement croissante sur l'intervalle [−6; −4].
La fonction g est strictement décroissante sur l'intervalle [−4; 1].
La fonction g est strictement croissante sur l'intervalle [1; 4].
La fonction g est strictement décroissante sur l'intervalle [4; 6].
III Tableau de variation
On résume le sens de variation d'une fonction dans un tableau de
variation.
Sur la première ligne du tableau on écrit l'ensemble de définition de la
fonction et les bornes des intervalles où la fonction est strictement
monotone (c'est à dire là où la fonction est strictement croissante ou
strictement décroissante).
Sur la deuxième ligne, des flèches indiquent le sens de variation de la
fonction sur chaque intervalle. A l' extrémité de chaque flèche on écrit les
images des bornes des intervalles.
Exemples : Tableaux de variation des fonctions f et g.
x
0 4 13
f(x)
5 9,5
3
x
−6 −4 1 4 6
g(x)
−1 1
−3 −4 −1
IV Maximum et minimum
Soit I un intervalle et f une fonction.
Le maximum de la fonction f sur I, s'il existe, est la plus grande valeur
prise par la fonction f sur I. C'est la plus grande des images.
Le minimum de la fonction f sur I, s'il existe, est la plus petite valeur
prise par la fonction f sur I. C'est la plus petite des images.
Page 2/3

Dire que la fonction f atteint son maximum en a sur I signifie que, pour
tout réel x de l'intervalle I, f(x) f(a).
Dire que la fonction f atteint son minimum en b sur I signifie que, pour
tout réel x de l'intervalle I, f(b) f(x).
On appelle extremum un nombre qui est un maximum ou un minimum.
Exemple :
Sur [−6; 6], le minimum de la fonction g est −4, il est atteint pour x = 1.
Sur [−6; 6], le maximum de la fonction g est 1, il est atteint pour x = 4.
Sur [−6; 1], le maximum de la fonction g est −1, il est atteint pour x = −4.
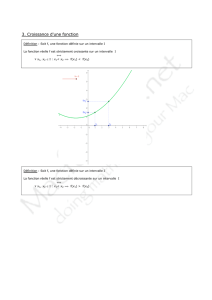
V Fonction strictement monotone sur un intervalle
Soit I un intervalle et f une fonction.
La fonction f est strictement croissante
sur I lorsque, pour tous nombres réels
u et v de I, si u < v alors f(u) < f(v).
Une fonction croissante conserve l'ordre.
Page 3/3
La fonction f est strictement
décroissante sur I lorsque, pour
tous nombres réels u et v de I,
si u < v alors f(u) > f(v).
Une fonction décroissante
renverse l'ordre.