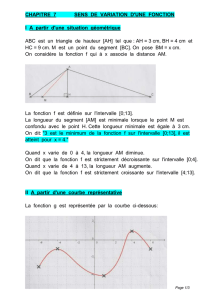
GENERALITES SUR LES FONCTIONS

Chapitre I
GENERALITES SUR LES FONCTIONS
I. RAPPELS SUR LES FONCTIONS
A) Définition
Définir une fonction c’est définir un procédé qui permet à tout nombre d’un intervalle donné
d’associer un autre nombre.
Remarque:
L'ensemble de définition de f est l'ensemble des réels qui ont une image par cette fonction. Il est
généralement noté Df.
B) Représentation graphique
Le plan est muni d’un repère (O,
i
,
j
).
Soit f une fonction définie sur l’intervalle I. On appelle courbe
représentative de f sur I, l’ensemble des points M(x,y) du plan tels que :
x I et ∈y = f(x)
Hélène Trouilhet 1/6
Une fonction définie sur un intervalle associe à chaque nombre de cet intervalle un
nombre réel et un seul . En mathématiques, on caractérise une fonction par la
notation suivante:
f : I ℝ
xfx
Ce qui signifie que la fonction f, définie sur un intervalle I, associe à tout réel x de
l'intervalle I, un unique réel noté f(x).
Si deux nombres réels y0 et x0 sont tels que y0 = f(x0), on dit que:
y0 est l'image de x0 par la fonction f
Ou que x0 est un antécédent de y0 par la fonction f
Remarque:
On note, le plus souvent, Cf la
courbe représentative de f.
On dit que la courbe Cf a pour
équation cartésienne y = f (x )
relativement au repère (O; i, j) .

Exemple et contre-exemple de courbe représentative d'une fonction:
C) Sens de variation d'une fonction
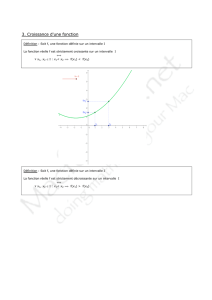
Soit f une fonction définie sur un intervalle I . On dit que :
●f est croissante ( resp. strictement croissante ) sur I , lorsque pour tous réels x et x’ de I ,
tels que x < x’ , on a f ( x )≤ f ( x’ ) (resp. f ( x ) < f ( x’ ) ) .
●f est décroissante ( resp. strictement décroissante ) sur I , lorsque pour tous réels x et x’
de I , tels que x < x’ , on a f ( x )≥ f ( x’ ) ( resp. f ( x ) > f ( x’ ) ) .
●f est monotone ( resp. strictement monotone ) sur I , lorsque f est soit croissante ( resp.
strictement ) sur I , soit décroissante ( resp. strictement ) sur I .
Remarque n°1:
En langage profane, on a pour habitude de dire qu’une fonction croissante conserve l’ordre, et une
fonction décroissante l’inverse.
Remarque n°2:
Etudier les variations d’une fonction, c’est préciser les intervalles sur lesquels la fonction est
monotone.On résume ces résultats dans un tableau appelé tableau de variations .
x–∞ –1 2 +∞
f(x)
3
–2
Hélène Trouilhet 2/6

II. LES FONCTIONS DE RÉFÉRENCE
Fonction Ensemble de définition, sens de variation Représentation graphique
Affine:
f : x axb
Df = ........
Si a > 0, f est croissante sur
ℝ
Si a < 0, f est ................ sur
ℝ
Carré:
f : x x2
Df = ........
f est croissante sur ........ et décroissante
sur.........
Remarque 1: ............
Remarque 2: ............
Cube:
f : x x3
Df = ........
f est ............ sur ........
Remarque: ............
Hélène Trouilhet 3/6
y = ........
y = ........

Inverse:
f : x 1
x
Df = ........
f est ...................
Remarque: ............
Racine carré:
f : x  x
Df = ........
f est .........
Valeur abolue:
f : x  ∣ x ∣
Df = ........
f est croissante sur ........ et décroissante
sur.........
Remarque:................
Cosinus:
f : x cosx
Df = ........
f est périodique de période ............
Sur l'intervalle
[0;2]
, f est croissante
sur ........ et décroissante sur.........
Remarque 1:................
Remarque 2:....................
Sinus:
f : x sin x
Df = ........
f est périodique de période ............
Sur l'intervalle
[0;2]
, f est croissante
sur ........ et décroissante sur.........
Remarque 1:................
Remarque 2:....................
Hélène Trouilhet 4/6

III. OPÉRATIONS SUR LES FONCTIONS
A) Somme, produit et quotient de fonctions
1. Définition:
Soient f et g deux fonctions définies respectivement sur Df et Dg , et k un réel non nul.
Opération Notation Définition Définie pour
Somme de deux
fonctions
fg
fgx= fxgx
x∈Df∩Dg
Produit d'une fonction
par un réel
kf
kf x=k×fx
x∈Df
Produit de deux
fonctions
f×g
f×gx= fx×gx
x∈Df∩Dg
Inverse
1
f
1
f=1 fx
x∈Df et fx≠0
Quotient
f
g
f
gx= fx gx
x∈Df∩Dq et gx≠0
Exemple: On considère les fonctions f: x → x + 1 définie sur et g: x →
1
x
définie sur .......
§ f + g est la fonction définie sur.........par ( f + g ) ( x ) = ..............
§ f g est la fonction définie sur ............ par (
f×g
) ( x ) = .............
§ 5f est la fonction définie sur ......... par ( 5 f ) ( x ) = .................
2. Sens de variation
Soient f et g deux fonctions monotones sur un intervalle I et k un réel non nul
§ Les fonctions f et f + k ont le même sens de variation sur I .
§ Si k > 0 , les fonctions f et k f ont le même sens de variation sur I .
§ Si k < 0 , les fonctions f et k f ont des sens de variation contraire sur I .
§ Si f et g sont strictement croissantes sur I , alors f + g est strictement croissante sur I .
§ Si f et g sont strictement décroissantes sur I , alors f + g est strictement décroissante sur I
Remarque:
Pour connaître le sens de variation de f – g, partir du sens de variation de f et de -g puis appliquer la
règle sur la somme car f+g = f + ( – g ) …
Attention!
Il est difficile d'établir des propriétés analogues pour les produits et quotients de fonctions!
Concernant le produit de deux fonctions, le signe de chaque fonction va aussi jouer un rôle dans le
sens de variation de la fonction produit.
Hélène Trouilhet 5/6