ADMIS MATHS C2

ADMIS MATHS C2
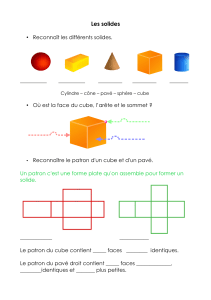
LES SOLIDES
CE1
Domaine : géométrie, les solides
Compétences : reconnaitre, décrire et nommer un cube et un pavé droit
On peut classer les solides en 2 familles :
- les polyèdres (plusieurs faces)
Est un solide délimité par un nombre fini de polygones, toutes ses faces sont des polygones
et donc sont planes.
Le plus petit est le tétraèdre (pyramide à base triangulaire)
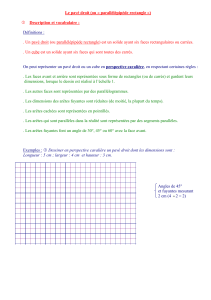
La perspective cavalière :
Dans un dessin en perspective cavalière, les longueurs et les angles ne sont pas conservés.
Elle conserve le parallélisme, le milieu d’un segment est représenté, les arêtes cachées sont en
pointillées
Pour décrire un polyèdre, on fait la liste de certaines de se caractéristiques (nbr de faces ….)
les sommets des polygones sont aussi les sommets du polyèdre, les côtés sont des arêtes, les
polygones sont les faces du polyèdre.
On appelle angle polyèdre : l’angle formé par toutes les faces adjacentes à un même sommet
La convexité :
Il existe plusieurs critères équivalents pour définir la convexité d’un polyèdre :
- un polyèdre est dit convexe si pour chaque plan de l’espace qui contient une face, le
polyèdre est tout entier = le polyèdre est situé entièrement d’un même côté par
rapport à l’une de ses faces
- un polyèdre est convexe quand toutes ses diagonales sont contenues à l’intérieur de
lui
- un polyèdre est convexe quand tout segment joignant 2 points situés à l’intérieur du
polyèdre
s’il n’est pas convexe alors il est concave
la formule d’ EULER
La relation d’Euler pour les polyèdres convexes est une égalité qui relie le nombre de face F ,
le nombre de sommets S, et le nombre d’arêtes A pour obtenir F + S = A + 2
Les polyèdres réguliers = est convexe tel que :
- toutes les faces sont des polygones réguliers identiques
- un nombre d’arêtes aboutit à chaque sommet = tous les angles sont égaux
ils sont 5 et sont appelés les solides de Platon :
- tétraèdre régulier 4 faces
- le cube 6 faces
- l’octaèdre 8 faces
- le dodécaèdre 12 faces
- l’icosaèdre 20 faces

un polyèdre est semi-régulier s’il est constitué de plusieurs sortes de polygones réguliers et
si tous ses sommets sont identiques
différents types de polyèdres :
prismes
pyramides
polyèdres composés (superposition de2 solides)
polyèdres tronqués (sommets sont coupés)
- les non polyèdres
ils peuvent rouler
ils ont des faces cylindriques
cylindre
cônes
sphère
patron d’un solide
Toute mise à plat de ce solide permettant de le reconstituer par pliage, sans recouvrement ni
trou = développement d’un solide
Le patron d’un solide n’est jamais unique ex : pour le cube il y a 11 patrons
De même que tous les solides n’ont pas nécessairement un patron ex : la sphère
Domaine GEOMETRIE
Les élèves apprennent à reconnaitre et à décrire des solides
Ils utilisent un vocabulaire spécifique
SCCC fin CE1
L’élève est capable de reconnaitre, nommer et décrire les solides usuels
Progression
- connaitre et utiliser un vocabulaire géométrique élémentaire approprié
- reconnaitre, décrire, nommer quelques solides droits : cube, pavé droit
SEQUENCE
Pré requis : reconnaitre et nommer le carré, le rectangle, le triangle, le cube et le pavé
droit
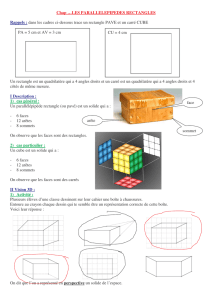
SEANCE 1 : cube et pavé droit
Objectif : reconnaitre, décrire et nommer un cube et un pavé droit
Déroulement :
Apporter des solides issus de la vie courante (boite de lait, …)
Demander aux élèves s’ils les connaissant les nommer et les décrire
Faire un tri parmi eux (polyèdre et non polyèdre)
Etablir des caractéristiques communes à chacun et les placer dans un tableau récapitulatif

Différence entre un cube et un pavé car tous les 2 ont 6 faces mais sont-elle identiques ?
Etablir les caractéristiques différentielles entre les 2 : le but étant de bien les reconnaitre
Nombre de faces
Nombres
d’arêtes
Nombre de
sommets
Forme des faces
Cube
Pavé droit
ATTENTION les cylindres, sphères et pyramides ne sont pas au programme du CE1
mais doivent quand même être vu pour bien comprendre les différentes faces que
composent les solides
SEANCE 2 : représentations planes d’un cube et d’un pavé droit
Objectif : reconnaitre les représentations en perspective cavalière d’un cube ou d’un
pavé droit
Déroulement :
Rappeler les caractéristiques des 2 élaborés lors de la séance 1
Prendre un solide de chaque en polystyrène et faire des empreintes sur du papier de chaque
face du solide (il doit y en avoir 6)
Faire le contour des faces au feutre noir
Proposer ensuite des photographie en perspective cavalière (cela peut être issu d’un manuel
de maths)
Demander aux élèves se qu’ils voient
Leur demander de faire la même représentation de leurs solides en polystyrène (à main levée)
Question : comment représenter les faces et les arêtes que l’ont ne voit pas ?
Par des pointillés = perspective cavalière
Découper leurs empruntes de solides faites en peinture et les coller sur une feuille de telle
sorte que les enfants devront tracer les perspectives cavalières
On peut ensuite proposer un patron de solide et demander aux enfants de le reconstituer, de
compter le nombre d’arêtes, sommets et de faces (les types de faces)
On peut proposer un jeu le qui suis-je ?