Les polyèdres réguliers convexes

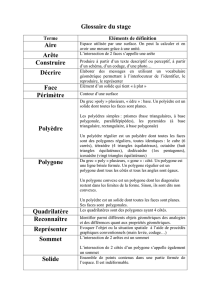
Polyèdres

Quelques définitions (1)
Un polyèdre* est un volume délimité par des faces
polygonales. (*poly:plusieurs, gone:angle, èdre:face)
Les polygones de deux faces consécutives ont un côté
commun appelé arête, leurs sommets communs sont
appelés sommets du polyèdre.

Quelques définitions (2)
Un polyèdre convexe est
un polyèdre entièrement
situé du même côté du
plan défini par une de ses
faces.
Un polyèdre étoile n’est
pas convexe : c’est un
polyèdre concave.

Catégories de polyèdres (1)
Parmi les différentes catégories de polyèdres,
on peut distinguer :
les
polyèdres réguliers
et les
polyèdres archimédiens.

Catégories de polyèdres (2)
Un polyèdre régulier est
un polyèdre dont les faces
sont des polygones
réguliers de même nature.
Wikipedia –Polyèdres
réguliers
Un polyèdre archimédien
ou semi-régulier est un
polyèdre dont les faces
sont des polygones
réguliers de natures
différentes.
Wikipedia –Polyèdres
archimédiens