Exercice 1

Seconde. Mathématiques. Interrogation écrite I 2.3.
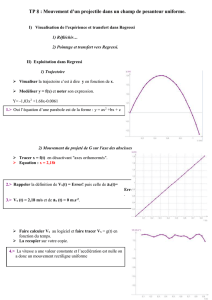
Exercice 1. Résoudre graphiquement le système (S1) : {2x – y = 5 ; x + 3y = – 1
Exercice 2. Résoudre par le calcul le système (S2) : {– 4x + 2y = –10 ; 3x + 9y = – 3
Exercice 3. (problème).
Alexandre dit à Belinda : « Donne-moi cinq de tes disques et nous en aurons autant l’un que l’autre ».
Bélinda répond : « Donne-moi dix disques et j’en aurai le double de ce qui te restera ».
Combien ont-ils de disques chacun.
● Seconde. Mathématiques. Interrogation écrite I 2.3.
Exercice 1. Résoudre graphiquement le système (S1) : {– 2x + y = – 5 ; – x – 3y = 1
Exercice 2. Résoudre par le calcul le système (S2) : { 4x – 2y = 10 ; 3x + 9y = – 3
Exercice 3. (problème).
Alexandre dit à Belinda : « Donne-moi cinq de tes disques et nous en aurons autant l’un que l’autre ».
Bélinda répond : « Donne-moi dix disques et j’en aurai le double de ce qui te restera ».
Combien ont-ils de disques chacun.
Seconde. Mathématiques. Correction Interrogation écrite I 2.3.
Exercice 1. Résolution graphique du système (S1) : {2x – y = 5 ; x + 3y = – 1
● 2x – y = 5  y = 2x – 5. Je reconnais l’équation d’une droite d1 non parallèle à (O ; ;j)

Pour tracer d1, il me faut construire deux points de cette droite.
Si x = 0 alors y = 2 × 0 – 5 = – 5 et par conséquent la droite d1 passe par le point A(0 ; – 5 )
Si x = 4 alors y = 2 × 4 – 5 = 3 et par conséquent la droite d1 passe par le point B(4 ; 3 )
● x + 3y = – 1  3y = – x – 1  y = –
Error!
x –
Error!
. Je reconnais l’équation d’une droite d2 non
parallèle à (O ; ;j)
Pour tracer d2, il me faut construire deux points de cette droite.
Si x = – 4 alors y = –
Error!
× (– 4) –
Error!
= 1 et par conséquent la droite d1 passe par le point
C(– 4 ; 1 )
Si x = 5 alors y = –
Error!
× 5 –
Error!
= – 2 et par conséquent la droite d1 passe par le point D(5 ;
– 2)
Je constate graphiquement que les droites d1 et d2 se coupent au point I(2 ;– 1)
Le couple (2 ;– 1) est donc l’unique solution du système (S1).
Exercice 2.
(S2)
{– 4x + 2y = –10 ; 3x + 9y = – 3
L1
L2
(S2) 
{– 4x + 2y = –10 ; 42 y = – 42
L1
L2 ← 3[L1] + 4[L2]
(S2)  {– 4x + 2 × (–1)= –10 ; y = – 1  {x = 2 ;y = – 1
Exercice 3. (problème).
Alexandre
Belinda
Équations
Situation initiale
x
y
1ère phrase
x + 5
y – 5
x + 5 = y – 5
2ième phrase
x – 10
y + 10
y + 10 = 2(x – 10)
Il nous faut donc résoudre le système (S3) {x = y – 10 ; y + 10 = 2x – 20 par substitution par exemple
(S3)  {x = y – 10 ; y + 10 = 2(y – 10) – 20  {x = y – 10; y = 50  {x = 40; y = 50
● Seconde. Mathématiques. Correction Interrogation écrite I 2.3.
Exercice 1. Résolution graphique du système (S1) : {– 2x + y = – 5 ; – x – 3y = 1
● – 2x + y = –5  y = 2x – 5. Je reconnais l’équation d’une droite d1 non parallèle à (O ; ;j)
Pour tracer d1, il me faut construire deux points de cette droite.
Si x = 0 alors y = 2 × 0 – 5 = – 5 et par conséquent la droite d1 passe par le point A(0 ; – 5 )

Si x = 4 alors y = 2 × 4 – 5 = 3 et par conséquent la droite d1 passe par le point B(4 ; 3 )
● – x – 3y = 1  3y = – x – 1  y = –
Error!
x –
Error!
. Je reconnais l’équation d’une droite d2 non
parallèle à (O ; ;j)
Pour tracer d2, il me faut construire deux points de cette droite.
Si x = – 4 alors y = –
Error!
× (– 4) –
Error!
= 1 et par conséquent la droite d1 passe par le point
C(– 4 ; 1 )
Si x = 5 alors y = –
Error!
× 5 –
Error!
= – 2 et par conséquent la droite d1 passe par le point D(5 ;
– 2)
Je constate graphiquement que les droites d1 et d2 se coupent au point I(2 ;– 1)
Le couple (2 ;– 1) est donc l’unique solution du système (S1).
Exercice 2.
(S2)
{ 4x – 2y = 10 ; 3x + 9y = – 3
L1
L2
(S2) 
{ 4x – 2y = 10 ; 42y = – 42
L1
L2 ← – 3[L1] + 4[L2]
(S2)  {4x – 2 × (–1) = 10 ; y = – 1  {x = 2 ;y = – 1
Exercice 3. (problème).
Alexandre
Belinda
Équations
Situation initiale
x
y
1ère phrase
x + 5
y – 5
x + 5 = y – 5
2ième phrase
x – 10
y + 10
y + 10 = 2(x – 10)
Il nous faut donc résoudre le système (S3) {x = y – 10 ; y + 10 = 2x – 20 par substitution par exemple
(S3)  {x = y – 10 ; y + 10 = 2(y – 10) – 20  {x = y – 10; y = 50  {x = 40; y = 50