03 - Trigonométrie dans le triangle rectangle

Chapitre 3 : Trigonométrie dans le triangle rectangle
3ème
Chapitre 3 : Trigonométrie dans le triangle rectangle
1
!
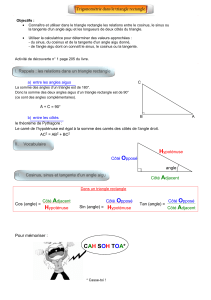
I. Rappel sur Pythagore
Exercice 1
ABCD est un rectangle de longueur
AB =7
cm et de largeur
AD =4
cm. Calculer la longueur de sa
diagonale AC.
Exercice 2
Calculer la longueur de la diagonale d’un carré de coté 6 cm.
Exercice 3
Le triangle RST est tel que
RS =3,9
cm,
ST =6,5
cm et
TR =5,2
cm.
Le triangle RST est-il rectangle ?
Exercice 4
Dans le triangle ABC, H est le pied de la hauteur issue de A. On donne
AB =25
cm,
AC =17
cm et
CH =8
cm.
1. Calculer AH puis BH.
2. Calculer l’aire du triangle ABC.
3. Le triangle ABC est-il rectangle ?
II. Cosinus sinus et tangente d’un angle aigu
1. Vocabulaire
On considère un triangle ABC rectangle en B.
L’angle
BAC
!
est un angle aigu de ce triangle.
•
AC
⎡
⎣⎤ ⎦
est le côté le plus long : c’est l’hypoténuse du triangle ABC.
•
AC
⎡
⎣⎤ ⎦
est le côté adjacent à l’angle
BAC
!
.
•
BC
⎡
⎣⎤ ⎦
est le côté opposé à l’angle
BAC
!
.
Faire de même pour le deuxième angle aigu du triangle.

3ème
Chapitre 3 : Trigonométrie dans le triangle rectangle
2
2. Définition
• Cosinus
Dans un triangle rectangle, le cosinus d'un angle aigu est le quotient de la longueur du côté
adjacent à cet angle par la longueur de l’hypoténuse.
• Sinus
Dans un triangle rectangle, le sinus d'un angle aigu est le quotient de la longueur du côté
opposé à cet angle par la longueur de l’hypoténuse.
• Tangente
Dans un triangle rectangle, la tangente d'un angle aigu est le quotient de la longueur du côté
opposé à cet angle par la longueur du côté adjacent.
Remarque
On retiendra la formule : CAH-SOH-TOA
Exercice 5
Dans le triangle RUN rectangle en U, on donne :
UN =4
cm et!
URN
!
=65°
.
1. Calculer RU.
2. Calculer RN.
3. Calculer l’angle
RNU
!
en utilisant un cosinus.
III. Propriétés du cosinus, du sinus et de la tangente d’un angle aigu
1. Propriétés du cosinus et du sinus
Le cosinus et le sinus d'un angle aigu sont des nombres strictement compris entre 0 et 1.
a désigne la mesure d’un angle aigu, on a :
0<cos a<1
! !et
0<sin a<1
.
2. Propriété de la tangente
La tangente d'un angle aigu est un nombre strictement positif.
a désigne la mesure d’un angle aigu, on a :
0<tan a

3ème
Chapitre 3 : Trigonométrie dans le triangle rectangle
3
3. Relations trigonométriques
a désigne la mesure d’un angle aigu, on a :
cos a
( )
⎡
⎣⎤ ⎦
2
+sin a
( )
⎡
⎣⎤ ⎦
2
=1
et !
tan a
( )
=
sin a
( )
cos a
( )
.
Applications
On donne
cos a
( )
=2
3
.
1. Calculer la valeur exacte de
sin a
( )
.
2. En déduire la valeur exacte de
tan a
( )
.
3. Reprendre les questions précédentes lorsque
sin a
( )
=1
2
.