1) Cinmatique du point

1re B et C 1 Cinématique du Point 1
Chapitre 1: Cinématique du Point
1. Position par rapport à un référentiel
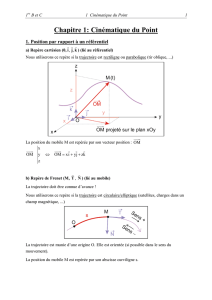
a) Repère cartésien (0, kji
G
G
G
, , ) (lié au référentiel)
Nous utiliserons ce repère si la trajectoire est rectiligne ou parabolique (tir oblique, ...)
La position du mobile M est repérée par son vecteur position : OM
J
JJJG
x
OM y OM xi yj zk
z
⇔=++
JJJJG JJJJGGGG
b) Repère de Frenet (M, N ,T
G
G
) (lié au mobile)
La trajectoire doit être connue d’avance !
Nous utiliserons ce repère si la trajectoire est circulaire/elliptique (satellites, charges dans un
champ magnétique, ...)
La trajectoire est munie d’une origine O. Elle est orientée (si possible dans le sens du
mouvement).
La position du mobile M est repérée par son abscisse curviligne s.

1re B et C 1 Cinématique du Point 2
Le repère de Frenet est lié au point M. Il comporte deux vecteurs unitaires et T
GN
G
:
• est tangent à la trajectoire au point M et orienté dans le sens de l’orientation de la
trajectoire.
T
G
• N
G
est perpendiculaire à T et dirigé vers l’intérieur de la concavité de la trajectoire.
G
Si la trajectoire n'est pas plane on ajoute un troisième vecteur unitaire k
G
perpendiculaire à T
G
et G.
N
2. Vitesse par rapport à un référentiel
a) Définition
d
t
OMd
t
OM
limv 0t
⎯→⎯⎯→⎯
→Δ =
Δ
Δ
=
G (1)
La vitesse instantanée v
G
est la dérivée de la position par rapport au temps.
⎯→⎯
OM
La vitesse exprime la rapidité avec laquelle la position varie.
Le vecteur vitesse est tangent à la trajectoire.
v
G

1re B et C 1 Cinématique du Point 3
b) Coordonnées cartésiennes
kvjvivv
v
v
v
v zyx
z
y
xGGG
GG ++=⇔ (2)
kzjyixOM
z
y
x
OM GGG ++=⇔ ⎯→⎯⎯→⎯ (3)
(1) et (3) ⇒ )kzjyix(
d
t
d
v
G
G
G
G
++=
k
dt
dz
j
dt
dy
i
dt
dx
v
G
G
G
G++= (4)
(2) et (4) ⇒ dt
dx
vx= dt
dy
vy= dt
dz
vz=
c) Coordonnées de Frenet
NvTvv
v
v
v NT
N
TGG
GG +=⇔
Comme est tangent à la trajectoire v
v
GN = 0 ⇒ T
vvT
=
⋅
G
G
Définition de la vitesse : 12
t0 t0
OM M M
vlim lim
tt
Δ→ Δ→
Δ
==
ΔΔ
JJJJG JJJJJJJG
G avec Δt = t2 – t1
Δt → 0 ⇒ ⇒
12
MM sT→Δ
JJJJJJJG G
t0
s
vlim T
t
Δ→
Δ
⎛⎞
=
⋅
⎜⎟
Δ
⎝⎠
G
G
Finalement T
d
t
ds
v
G
G
= ⇒ d
t
ds
vT= et vN = 0

1re B et C 1 Cinématique du Point 4
d) Vitesse linéaire et vitesse angulaire dans le cas du mouvement circulaire uniforme
Un mobile M se déplace à vitesse constante v sur une trajectoire circulaire de rayon R.
Origine des temps et des espaces: à t = 0, M se trouve à l'origine O de la trajectoire circulaire
que l'on oriente dans le sens du mouvement.
La position du mobile peut être repérée soit par son abscisse curviligne s, soit par son
abscisse angulaire θ qui mesure l'angle de la rotation depuis l'origine O sur le cercle.
A l'instant t1, son abscisse
curviligne est s1, à l'instant t2, il est
s2. Son déplacement pendant la
durée Δt = t2 − t1 est Δs = s2 − s1.
A l'instant t1, son abscisse
angulaire est θ1. (C'est l'angle entre
CO et CM1.) A l'instant t2, il est θ2.
Son angle de rotation pendant la
durée Δt = t2 − t1 est Δθ = θ2 − θ1.
La mesure de l'abscisse angulaire θ
est positive si la trajectoire du
point a été orientée dans le sens du
mouvement ! Cette mesure s'exprime en radians (rad) dans le Système International d'unités.
• Relation entre l’arc et l’angle:
, où Δθ est exprimé en rad
sRΔ= ⋅Δθ
Le radian est donc l'angle pour lequel l'arc est égal au rayon.
Pour 1 tour complet, Δs = 2πR.
On a donc: 1 tour = 360° = 2π rad.
• Vitesse linéaire v (instantanée):
C'est la vitesse instantanée de M: dt
ds
vv T== .
Dans le cas du mouvement uniforme s
vt
Δ
=
Δ
(formule vue en classe de 2e)

1re B et C 1 Cinématique du Point 5
• Vitesse angulaire ω (instantanée):
C'est l'angle duquel M tourne par unité de temps: t0
d
lim tdt
Δ→
Δ
θθ
ω= =
Δ
Dans le cas du mouvement uniforme t
Δ
θ
ω=
Δ
(formule à retenir)
Unité S.I.: 1 rad/s.
• Relation entre vitesse linéaire et vitesse angulaire d'un point:
sR
vR
tt t
Δ ⋅Δθ Δθ
= = =⋅ =⋅ω
ΔΔ Δ
R
Finalement: vR
=
⋅ω (formule à retenir)
• Période de rotation T
C'est la durée d'1 tour:
t T si 2Δ= Δθ= π
2
T
π
ω= ⇔ Période 2
Tπ =ω (formule à retenir)
• Fréquence de rotation f
C'est le nombre de tours par seconde.
En T secondes il y a 1 tour
En 1 seconde il y a 1/T tours
Fréquence 1
fT = exprimée en hertz (Hz) (formule à retenir)