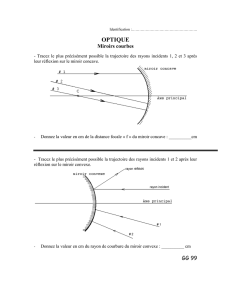
Chp.9 Fonctions convexes

Fonctions convexes
Prologue
Ce chapître développe les propriétés des fonctions convexes f∶C⊂E↦R
définies sur une partie convexe Cd’un espace de dimension finie E. Si, fonda-
mentalement, la convexité est une propriété unidimensionnelle - une fonction
f∶C⊂E↦Rest convexe si et seulement si, pour toute droite affine (D)de E,
sa restriction à (D)∩Cest convexe - l’exigence que cette propriété soit vérifiée
dans toutes les directions, c’est-à-dire pour toute droite affine (D), contraint la
fonction fà une certaine régularité globale. On prouve par exemple que toute
fonction convexe f∶C⊂E↦Rest localement Lipschitzienne sur l’intérieur de
son domaine C(Corollaire 9.4.1), et qu’elle est Fréchet-dérivable en tout point
ade l’intérieur de Cen lequel elle admet des directionnelles dans les directions
des nvecteurs d’une quelconque base B={e(1),...,e(n)} de E. En particu-
lier, f∶C⊂Rn↦Rest Fréchet-dérivable en un point ade l’intérieur de C, dès
qu’elle admet des dérivées partielles en a(Corollaire 9.4.2).
On caractérise les fonctions convexes f∶C⊂E↦Rdeux-fois Fréchet-dériva-
bles sur un ouvert convexe Ccomme les fonctions dont la dérivée seconde, en
tout point de C, est une forme bilinéaire SDP , et on énonce alors une condi-
tion nécessaire et suffisante pour qu’une telle fonction fsoit strictement convexe
(Corollaire 9.5.1).
La convexité joue un rôle central en optimisation pour au moins deux rai-
sons fondamentales. La première est que l’on sait écrire, pour tout problème
d’optimisation convexe, c’est-à-dire tout problème consistant à minimiser une
fonction convexe sur un ensemble convexe, des conditions nécessaires et suffi-
santes d’optimalité (Théorème 9.3.2). La seconde, plus pragmatique, est que, s’il
existe des algorithmes bien adaptés à la résolution numérique des problèmes
convexes, les problèmes non convexes s’avèrent extrèmement difficiles à ré-
soudre numériquement, et nécessitent le recours à des heuristiques(1)ou à des
méthodes stochastiques(2).
1. Heuristique : du grec : ²υρισκω : « je trouve » : méthode de calcul fournissant en temps
polynômial une solution réalisable non nécessairement optimale d’un problème d’optimisation.
2. Stochastique : Se dit des phénomènes relevant du hasard, et faisant l’objet d’une analyse
statistique : http : // larousse.fr/dictionnaires/français/stochastique/74742 .

224 CHAPITRE 9. FONCTIONS CONVEXES
tAvertissement : Dans toute cette partie, Edésigne toujours un espace de dimension
finie, Dune partie quelconque de E, et Cune partie convexe de E, contenue dans D.
On rappelle qu’une partie Cde Eest « convexe » si et seulement si :
a,c∈C, ,0 ≤t≤1⇒t b +(1−t)a∈C
9.1 Fonctions convexes et fonctions affines
Fonctions convexes
Définition 9.1.1 f∶C⊂E↦Rest dite « convexe » (resp. « concave ») si, pour tout
couple de points distincts a et b de C , et tout réel t strictement compris entre zéro
et un :
f(t b +(1−t)a)≤t f (b)+(1−t)f(a) (resp. ≥)(9.1)
et « strictement convexe » (resp. « strictement concave ») si :
f(t b +(1−t)a)<t f (b)+(1−t)f(a) (resp. >)(9.2)
f∶D⊂E↦Rest dite « convexe (resp. concave, strictement convexe, strictement
concave) sur C », si C est une partie convexe contenue dans D, et si la restriction
de f à C est convexe (resp. concave, strictement convexe, strictement concave)
tfest donc concave (resp. strictement concave) si et seulement si (-f) est convexe (resp.
strictement convexe).
Proposition 9.1.1 Si f ∶C⊂E↦Rest convexe, stous es ensembles de niveau :
Sc(f)={x∈Cf(x)≤c} (c∈R)(9.3)
sont convexes (éventuellement vides).
Preuve : C’est une conséquence directe de (9.1).
Fonctions affines
Définition 9.1.2 Une fonction f ∶C⊂E↦F est dite « affine » si, pour tout couple
de points distincts a et b de C , et tout réel t strictement compris entre zéro et un :
f(t b +(1−t)a)=t f (b)+(1−t)f(a)(9.4)
Une fonction f ∶D⊂E↦F est dite « affine sur C » si C est une partie convexe
contenue dans D, et si la restriction de f à C est affine.
tUne fonction affine à valeurs réelles est une fonction à la fois convexe et concave.

9.1. FONCTIONS CONVEXES ET FONCTIONS AFFINES 225
Proposition 9.1.2 (Admise) Une fonction f ∶C⊂E↦F est affine si et seulement
si on peut trouver une application linéaire L ∶E↦F et un élément y dans F tels
que, pour tout x dans C : g (x)=L(x)+y. Lorsque C est d’intérieur non vide dans
E , L et y sont définis de manière unique.
tToute fonction affine définie sur une partie convexe Cde Rn, à valeurs dans Rm,
est de la forme :
f∶C⊂Rn↦Rm∶x↦A⋆x+b
où Aest une m×nmatrice réelle, et bun vecteur de Rmdonnés. Lorsque Cest
d’intérieur non vide, Aet bsont définis de manière unique.
Inégalité de Jensen
Théorème 9.1.1 (Inégalité de Jensen(3))Si f ∶C⊂E↦Rest convexe :
f(n
k=1
α(k)a(k))≤n
k=1)
α(k)f(a(k)) (9.5)
pour toute suite finie de points a(k)(1≤k≤n ) de C , et toute combinaison
convexe :
n
k=1
α(k)a(k)des a(k).
Preuve : Pour tout entier n, et toute suite a(k)(1 ≤k≤n) de points de C, po-
sons :
Σ(n)={α=α(1),...,α(n)α(i)=0(i≤1≤n),
n
k=1
α(k)=1}
et :
Ca(1), .. ., a(n)={α∈Σ(n)  f(n
k=1
α(k)a(k))≤n
k=1
α(k)f(a(k))}
Il s’agit de prouver que, pour tout entier n, et toute suite a(k)( 1 ≤k≤n) de
points de C:Ca(1), . .. , a(n)=Σ(n). Mais Ca(1), .. ., a(n)est convexe,
3. - Johan Ludwig Jensen, 1859-1925, Mathématicien amateur Danois, essentiellement autodi-
dacte, employé par la succursale Danoise de l’International Bell Telephone Company. L’in-
égalité de Jensen apparait pour la première fois en 1906 dans un article publié par Jensen
dans la revue Acta Mathematica. Pour découvrir sa biographie : http://www-groups.dcs.st-
andrews.ac.uk/history/Biographies/Jensen.html.

226 CHAPITRE 9. FONCTIONS CONVEXES
puisque : α,β∈Σ(n),α≠β, et : 0 <t<1 impliquent :
fn
k=1tα(k)+(1−t)β(k)a(k)=ft
n
k=1
α(k)a(k)+(1−t)n
k=1
β(k)a(k)
... ≤t f (n
k=1
α(k)a(k))+(1−t)f(n
k=1
β(k)a(k))
... ≤t
n
k=1
α(k)f(a(k))+(1−t)n
k=1)
α(k)f(a(k))
... =n
k=1tα(k)+(1−t)β(k)f(a(k))
et contient tous les sommets de Σ(n), donc : Ca(1), ..., a(n)=Σ(n).
Opérations sur les fonctions convexes
Proposition 9.1.3 Si f ∶C⊂E↦Ret g ∶C⊂E↦Rsont convexes (resp. concaves) :
f+g∶C⊂E↦R∶x↦f(x)+g(x)
l’est aussi. Si en outre f ou g est strictement convexe (resp. strictement concave),
f+g l’est également.
Proposition 9.1.4 (Composition à gauche) Si : f∶C⊂E↦Rest convexe (resp.
concave), f(C)est contenu dans un intervalle Ide R, et ϕ∶I⊂R↦Rest
convexe (resp. concave) croissante :
ϕ○f∶C⊂E↦R
est convexe. Si en outre fest strictement convexe (resp. strictement concave)
et ϕstrictement croissante , g○fest strictement convexe (resp. strictement
concave).
Exemple 9.1.1 Pour toute n ×n matrice réelle symétrique Q, et tout vecteur r de
Rn, O ={x∈Rnx′⋆Q⋆x−r′⋆x<0}est un ouvert convexe de Rn, et :
f∶O⊂Rn↦R∶x↦ln(r′⋆x−x′⋆Q⋆x)
est concave (resp. strictement concave) dès que Q est SDP (resp. DP) (Exercice 9.5).
BLe produit de deux fonctions convexes sur Cn’est pas en général une fonction convexe
sur C.

9.2. EXISTENCE DE DEMI-DÉRIVÉES DIRECTIONNELLES 227
Exemple 9.1.2 f∶R2↦R∶(x1x2)↦x1x2est le produit de deux fonctions linéaires
mais n’est convexe sur aucun ouvert convexe de R2.
Proposition 9.1.5 (Composition à droite) Si g∶C⊂E↦Fest affine, et
f∶g(C)⊂F↦Rest convexe, f○g∶C⊂E↦Rest convexe (resp. concave). Si en
outre gest injective et fstrictement convexe, (resp. strictement concave) f○g
est strictement convexe (resp. strictement concave).
Exemple 9.1.3 Pour toute suite finie de N vecteurs : p(k)(1≤k≤N ) de Rn, et
toute suite de N réels q(k)i (1≤k≤N), la fonction :
f∶C⊂Rn↦R∶x↦N
k=1
ln(q(k)−p(k)′⋆x)
où : C ={x∈Rnp(k)′⋆x<q(k) (1≤k≤N)}, est concave. Elle est strictement
concave sur C lorsque le rang du système des N vecteurs p(k)est : n ≤N.
9.2 Existence de demi-dérivées directionnelles
Théorème 9.2.1 Soit f ∶C⊂E↦Rune fonction convexe, et a un point de l’inté-
rieur de C .
1. f admet une « demi-dérivée directionnelle » :
D f (a,υ)=lim
t→0+
t−1([f(a+tυ)−f(a)] (9.6)
au point a dans la direction de tout vecteur υde E .
2. D f (a)∶E↦R∶υ↦D f (a,υ)est une fonction convexe, homogène de de-
gré un.
3. Pour tout point x dans C :
f(a)+D f (a,x−a)≤f(x)(9.7)
et l’inégalité est stricte dès que f est strictement convexe et x distinct de a .
Preuve : - 1. Soient υun vecteur quelconque de Eet tun réel strictement posi-
tif assez petit pour que : 0 <s<t⇒a+sυ∈C(un tel texiste toujours puisque
aest supposé appartenir à l’intérieur de C). Pour tout couple de réels set rde
l’intervalle ouvert ]0, t[, tels que : s<r, il existe un réel θ, strictement compris
entre zéro et un, tel que : s=θr, d’où :
f(a+sυ)=f(a+θrυ)=f((1−θ)a+θ(a+rυ)) ≤(1−θ)f(a)+θf(a+rυ)