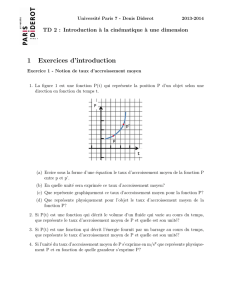
Classification des formes quadratiques `a coefficients rationnels

Universit´e Henri Poincar´e
Facult´e de math´ematiques M´emoire de Master-1
Dirig´e par Fr´ed´eric Campana
Classification des formes quadratiques ` a coefficients rationnels
Pierre-William Martelli
Saint-Max, le 15 juin 2010

2

Table des mati`eres
Introduction 4
1 Formes quadratiques 5
1.1 G´en´eralit´es . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2 Orthogonalit´e ........................................................ 7
1.3 Vecteurs isotropes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.4 Bases orthogonales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
1.5 Th´eor`eme de Witt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
1.6 Traductions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
1.7 Formes quadratiques sur Fq. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2 Formes quadratiques sur Q22
2.1 Quelques rappels . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.1.1 Quelques r´esultats sur le corps Qp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.1.2 Symbole de Hilbert . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.1.3 Formes quadratiques sur Qp. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.2 Invariants d’une forme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.3 Classification . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
2.4 Applications . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Conclusion 36
Bibliographie 37
3

Introduction
C’est `a l’occasion de second Congr`es International des math´ematiciens, le 8 aoˆut 1900 `a Paris, que le c´el`ebre David
Hilbert a ´enonc´e `a 226 de ses confr`eres pr´esents, une liste de 23 probl`emes. L’un de ces probl`emes, le onzi`eme, demande :
Peut-on obtenir une classification des formes quadratiques `a coefficients dans un anneau d’entiers alg´ebriques
semblable `a la classification usuelle sur R?
L’objectif de ce travail est de donner une r´eponse partielle `a cette question, en exploitant abondamment [Ser70] pour
cela. Notre r´eponse ne sera que partielle car nous n’allons pas travailler sur un anneau d’entiers alg´ebriques quelconques,
mais sur le corps des rationnels Q.
Ce m´emoire se divise en deux chapitres. Dans le premier, nous donnerons quelques r´esultats g´en´eraux sur les formes
quadratiques. Dans le second, nous ferons quelques rappels succincts sur le corps des nombres p-adiques et la classification
des formes quadratiques sur ces corps. Enfin l’objectif de ce m´emoire sera atteint avec le th´eor`eme de Hasse-Minkowski.
Je tiens `a remercier M. Campana pour le temps qu’il m’a consacr´e, ainsi que l’´energie d´eploy´ee pour maximiser la
qualit´e de ce travail.
4

Chapitre 1
Formes quadratiques
Dans cette partie nous introduisons les notions de forme quadratique et d’´equivalence entre formes quadratiques. C’est
cette notion qui nous permettra d’´etablir des r´esultats de classification sur les formes quadratiques. Nous d´emontrerons
en outre le th´eor`eme de Witt et nous admettrons le th´eor`eme de Chevalley-Warning, que nous appliquerons aux formes
quadratiques d´efinies sur les corps finis.
1.1 G´en´eralit´es
D´efinition 1.1.1 (Module)
Soient Aun anneau commutatif et (M, +)un groupe ab´elien. Mest dit module sur A(ou A-module) s’il est muni
d’une loi externe ⋅∶A×MÐ→Mv´erifiant, pour tous (a, b)∈A2,(x, y)∈M2,
1. a⋅(x+y)=a⋅x+a⋅y
2. (a+b)⋅x=a⋅x+b⋅x
3. (ab)⋅x=a(b⋅x)
4. 1⋅x=x
Exemple 1 1. Si kest un corps, un k-module et un k-espace vectoriel sont les mˆemes objets.
2. L’ensemble des vecteurs du plan dont les coordonn´ees sont dans Zforme un Z-module.
3. Soit Gun groupe ab´elien. L’action ϕ∶G×ZÐ→ G
(x, n)z→ nx
munit Gd’une structure naturelle de Z-module.
D´efinition 1.1.2 (Forme quadratique)
Soient Aun anneau commutatif et Vun module sur A. Une application Q∶VÐ→Aest appel´ee forme quadratique
sur Vsi :
1. On a pour tous a∈A,x∈V,Q(ax)=a2Q(x).
2. L’application (x, y)z→Q(x+y)−Q(x)−Q(y)est une forme bilin´eaire.
Un tel couple (V, Q)est appel´e un module quadratique.
Dans tout ce chapitre, kd´esignera d´esormais un corps de caract´eristique diff´erente de 2, Vun k-espace vectoriel de
dimension n∈N⋆et (V, q)un module quadratique.
Exemple 2 1. L’ensemble des formes quadratiques sur Vest un k-espace vectoriel.
2. Soient Bune base de V,xun vecteur de coordonn´ees (x1, ..., xn)dans B,f∶xz→ n
i=1
x2
i. Alors (V, f)est un module
quadratique.
3. Soit ϕ∈V⋆. Alors ϕ2est une forme quadratique.
5