Algorithme d`Euclide

[email protected] licence CC-BY-NC-SA
DUT Informatique
semestre 4
arithm´etique/cryptographie
L’algorithme d’Euclide
Math´ematiques
TP n◦1
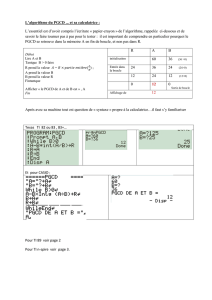
La principale primitive Scilab utile en arithm´etique est pmodulo(a,b) renvoie le reste
de la division Euclidienne de apar b. Par exemple :
-->//calcul du reste de 15437/531
-->pmodulo(15437,531)
ans =
38.
-->//calcul du quotient de 15437/531
-->(15437-38)/531
ans =
29.
ce qui signifie que 15437 = 531 ×29 + 38. Dans les TP qui vont suivre nous utiliserons
Scilab pour mettre en œuvre certains algorithmes d’arithm´etique.
Exercice 1
Algorithme d’Euclide
On rappelle l’algorithme d’Euclide pour calculer le PGCD de deux nombres
✬
✫
✩
✪
fonction d=PGCD(a, b)
tant que reste 6= 0 faire
faire la division Euclidienne de apar b
remplacer apar bet bpar reste
fin faire
d= dernier reste non-nul
.
1. Appliquer cet algorithme `a 48 et 27. Dans quelle variable se trouve le PGCD(a, b)
`a la fin de l’algorithme ?
2. Cr´eer une fonction scilab calculant le PGCD(a, b) suivant cet algorithme et tester.
3. Modifier cette fonction pour afficher chaque ligne du calcul dans la console.
Indication : Utilisation de printf :
printf(’ins`ere %d puis %d dans du texte\n passage `a la ligne ’,123,456)
donne comme r´esultat :
--> printf(’ins`ere %d puis %d dans du texte\n passage `a la ligne ’,123,456)
ins`ere 123 puis 456 dans du texte
passage `a la ligne
4. Si a≥bque se passe-t-il lors du premier passage dans la boucle tant que ?
1

[email protected] licence CC-BY-NC-SA
DUT Informatique
semestre 4
arithm´etique/cryptographie
L’algorithme d’Euclide
Math´ematiques
TP n◦1
Exercice 2
Identit´es de Bezout
Nous avons vu qu’`a partir des calculs fait dans l’algorithme d’Euclide on peut obtenir
des identit´es de Bezout utiles dans la r´esolution de certains probl`emes d’arithm´etique.
L’algorithme d’Euclide consiste `a calculer le reste rk+1 de la division Euclidienne de rk−1
par rkjusqu’`a obtenir 0, avec par convention r−1=aet r0=b.` A partir de toutes
les ´equations obtenues on peut, en repartant de l’´etape nexprimer rn= PGCD(a, b) en
fonction de rn−1et rn−2puis de rn−2,rn−3rn−4. . .et enfin seulement en fonction de aet b.
Notre probl`eme consiste `a trouver une version it´erative de cet algorithme vu en cours. On
va donc construire, parall`element au d´eroulement de l’algorithme d’Euclide, deux suites
(ui)i=−1,...n et (vi)i=−1,...n telles que
∀i=−1,0. . . n, ri=a×ui+b×vi
de sorte que l’identit´e de Bezout soit donn´ee par la ni`eme ´etape de calcul :
a=a×1 + b×0 ´etape -1
b=a×0 + b×1 ´etape 0
r−1=a=b×q1+r1r1=a×1 + b×(−q1) ´etape 1
r0=b=r1×q2+r2r2=a×(−q1) + b×(1 + q1q2) ´etape 2
.
.
..
.
..
.
..
.
..
.
..
.
.
ri−3=ri−2×qi−1+ri−1ri−1=a×ui−1+b×vi−1´etape i-1
ri−2=ri−1×qi+riri=a×ui+b×vi´etape i
ri−1=ri×qi+1 +ri+1 ri+1 =a×ui+1 +b×vi+1 ´etape i+1
.
.
..
.
..
.
..
.
..
.
..
.
.
rn−2=rn−1×qn+rnrn=a×un+b×vn´etape n
rn−1=rn×qn+1 + 0 rn+1 =a×un+1 +b×vn+1 ´etape n+1
Les ´etapes −1 et 0 servent `a initialiser les calculs. Nous allons voir comment passer
des ´etapes i−1 et i`a l’´etape i+ 1.
1. Rappeler comment on calcule ri+1 et qi+1 en fonction de riet ri−1en utilisant
seulement les fonctions scilab pmodulo,+,-,*,/ ?
Indication : il s’agit de l’´etape i+ 1 de l’algorithme d’Euclide (??) :
ri−1=ri×qi+1 +ri+1
2. Comment sont initialis´ee les suites (ri)i=−1,0,...n,(ui)i=−1,0,...n et (vi)i=−1,0,...n ?
3. Combiner les ´equations obtenues aux ´etapes i−1 et ipour obtenir l’´equation
de l’´etape i+ 1. En d´eduire les formules de calcul de ui+1, vi+1 en fonction de
ui, ui−1, vi, vi−1et qi+1 ?
Indication : comme dans la m´ethode de Gauss trouver les coefficients `a utiliser
pour obtenir l’´etape i+ 1 en utilisant les ´etapes iet i−1:
ri−1=a×ui−1+b×vi−1
ri=a×ui+b×vi
ri+1 =a×... +b×...
les coefficients seront trouv´es en utilisant la division Euclidienne :
ri+1 =ri−1−ri×qi+1
2

[email protected] licence CC-BY-NC-SA
DUT Informatique
semestre 4
arithm´etique/cryptographie
L’algorithme d’Euclide
Math´ematiques
TP n◦1
4. Quel test permet d’arrˆeter le calcul ?
5. ´ Ecrire la fonction Scilab
Bezout :Z×Z−→ Z×Z×Z
a, b 7−→ u, v, d tels que au +bv =d
Attention il faut retenir deux lignes cons´ecutives du calcul, les ´etapes iet i−1,
pour en calculer une troisi`eme, ´etape i+ 1, pour cela il nous faut 10 variables. On
prendra les notations suivantes : qpour le quotient qi+1 et
r0:= valeur de ri−1u0:= valeur de ui−1v0:= valeur de vi−1
r1:= valeur de riu1:= valeur de uiv1:= valeur de vi
r:= valeur de ri+1 u:= valeur de ui+1 v:= valeur de vi+1
6. Mettre en œuvre un test prouvant la validit´e des r´esultats donn´ees par Bezout. ` A
partir de quelle taille de chiffres l’algorithme ne marche-t-il plus ?
Exercice 3
PGCD r´ecursif
1. ´ Ecrire une fonction scilab d=PGCD rec(a,b) qui calcule le PGCD(a, b) de mani`ere
r´ecursive : ✬
✫
✩
✪
fonction d=PGCD rec(a, b)
si b= 0 alors d=a
sinon r= reste de adivis´e par b
d=PGCD rec(b, r)
fin
2. Modifier la fonction, `a l’aide de la commande printf, pour faire apparaˆıtre les
diff´erents PGCD calcul´es.
3. Tester la fonction avec PGCD(27,48)
Exercice 4
Identit´es de Bezout [TP not´e 2010,8pts]
1. ´ Ecrire une fonction [R,Q]=Euclide(a,b) qui renvoie la liste Rdes restes et celle
Qdes quotients obtenus lors du calcul du PGCD(a, b). Pour a= 48 et b= 27 on
devrait obtenir :
R=[48; 27; 21; 6; 3; 0] et Q=[0; 0; 1; 1; 3; 2]
Indication : il suffit de stocker convenablement les restes et quotients calcul´es
dans la fonction PGCD du TP1.
2. ´ Ecrire une fonction ligne bezout(C,R) qui affiche dans la console scilab l’´equation
stock´ee dans les matrices Cet Rd´efinie par PGCD(a, b) = PiC(i)×R(i). Par
exemple :
R= [48;27;21;6;3;0],C= [0;0;1;−3;0;0]−−−−−−−−−−→
ligne bezout 3 = 21 + 6 ×(−3)
Indication : Pour afficher une ligne dans la console on pourra utiliser prinft().
3

[email protected] licence CC-BY-NC-SA
DUT Informatique
semestre 4
arithm´etique/cryptographie
L’algorithme d’Euclide
Math´ematiques
TP n◦1
Pour plus de lisibilit´e, mettre des parenth`eses autour de C(i) qui peut ˆetre n´egatif.
Rrepr´esente la liste des restes de l’algorithme d’Euclide, donc a, b et PGCD(a, b)
sont d´ej`a contenus dans Ret n’ont pas besoin d’ˆetre recalcul´e.
3. ´ Ecrire une fonction bool=verifie ligne bezout(C,R) qui renvoie :
%T si on a bien PGCD(a, b) = PiC(i)×R(i) et%F sinon.
Indication : on doit tester que le R(i) = PGCD(a, b)dans Rest bien le PGCD(a, b)
et que la somme PiC(i)×R(i)est bien ´egale `a ce PGCD(a, b)
4. ´ Ecrire une fonction [u,v,d]=Bezout TD(a,b) qui calcule les coefficients d’une
identit´e de Bezout au +bv =dentre les nombres aet b`a partir de la m´ethode
utilis´ee en TD (cf. ci-dessous). On affichera chaque ligne du calcul dans la console
de scilab.
✬
✫
✩
✪
fonction [u, v, d] = Bezout TD(a, b)
Calculer la liste Rdes restes, celle Qdes quotients,
et d= PGCD(a, b) par l’algorithme d’Euclide
R= [a,b,r1,...,rn−1,rn,0]; Q= [0,0,q1,...,qn−1,qn,qn+1]
initialiser la liste des coefficients Ctelle que d=PiC(i)×R(i)
en partant de l’´equation d= 1 ×rn, ce qui donne :
C= [0,0,0,..., 0,1,0]
tant que Cn’est pas de la forme [u,v,0,...,0]faire
modifier Cen utilisant les r`egles de simplification
obtenues `a chaque ´etape de l’algorithme d’Euclide :
pour i= 3 jusqu’`a fin de Cfaire
modifier C(i-2) , C(i-1) et C(i) avec
ri=ri−2−ri−1×qi
fin faire
afficher dans la console la nouvelle ´equation obtenue
fin faire
r´ecup´erer les coefficients de l’identit´e de Bezout au +bv =d
Indication : Pour faciliter la conception de la fonction on utilisera :
•bool=verifie ligne bezout(C,R) pour v´erifier les calculs `a chaque ´etape
•ligne bezout(C,R) pour afficher l’´equation dans la console
4