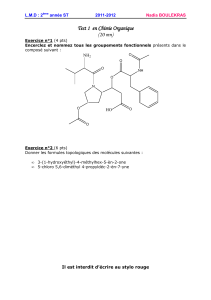
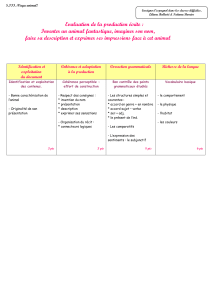
L`intra 2 avec une solutionnaire - Département de mathématiques et

Faculté des arts et des sciences
Département de mathématiques et de statistique
Sigle du cours : MAT1500
Titre du cours : Mathématiques discrètes
Professeur : Abraham Broer
Date de l’intra 2 : Le 16 mars 2017, 13h30 à 15h20
Directions pédagogiques: Aucune documentation permise. Calculatrice simple est permise.
Justifier toujours vos réponses.
1a) [4 pts] Utiliser l’algorithme de Bézout/Euclide pour trouver pgcd(931,1323),ppcm(931,1323)
et deux nombres entiers s0, t0tels que
931s0+ 1323t0= pgcd(931,1323).
Réponse. Par Euclide/Bézout :
1·1323 + 0 ·931 = 1323
0·1323 + 1 ·931 = 931
1·1323 + (−1) ·931 = 392 (= 1323 −931)
(−2) ·1323 + (3) ·931 = 147 (= 931 −2·392)
(5) ·1323 + (−7) ·931 = 98 (= 392 −2·147)
(−7) ·1323 + (10) ·931 = 49 (= 147 −1·98)
et 98 = 2 ·49 + 0.
Donc pgcd(931,1323) = 49,ppcm(931,1323) = 931·1323
49 = 25137,s0= 10 et t0=−7.
1b) [3 pts] Trouver un nombre naturel N > 0tel que
(1323 ·N)≡931 147
Réponse. Par 1a) (−7) ·1323 + 10 ·931 = 49, donc après multiplication par 3on obtient
(−21) ·1323 + (30) ·931 = 147.
Parce que 931|30·931 on a (−21)·1323 ≡931 147. On a (−21) ≡931 910, donc aussi 910·1323 ≡931 147.
Donc réponse : N= 910.
1c) [3 pts] Soient aet bdeux nombres entiers non-zéro. Supposons qu’ils existent six nombres
entiers s1, s2, t1, t2, u16= 0, u26= 0 tels que s1a+t1b=u1,s2a+t2b=u2et pgcd(u1, u2)=1.
Montrer : pgcd(a, b)=1.
1

2
Réponse. Soit d= pgcd(a, b). Alors d|aet d|bdonc d|(s1a+t1b),d|(s2a+t2b)et donc d|u1et d|u2
et dest un diviseur en commun de u1et u2. Mais 1est le seul diviseur en commun positif, parce
que pgcd(u1, u2)=1. Donc d= 1.
2a) [3 pts] Écrire N= [999]16 + 1 sur la base 16 et sur la base 10. Écrire M= [1000]7·[7]2
10 −1sur
la base 7. Écrire P= [1000]10 sur la base 7. (Montrer vos calculs.)
Réponse. N= [999]16 +1 = [9,9,9,10]16 = [999A]16 = (9·162+9·161+9)+ 1 = 2457 +1 = 2458.
M= [1000]7·[7]2
10 −1 = [100000]7−1 = [66666]7,parce que
[66666]7+1 = (6·74+6·73+6·72+6·71+6)+1 = (6·74+6·73+6·72+6·71+7) = (6·74+6·73+6·72+72) =
(6 ·74+ 6 ·73+ 73) = (6 ·74+ 74)=75= [100000]7.
On a P= [2626]7parce que 1000 = 142 ·7+2,142 = 20 ·7+2,20 = 2 ·7+6,2=2·7+0.
2b) [3 pts] Soient b, r des entiers tel que b≥r > 6et r≡16 b. Posons N:= [5,4,3,2,1]bet
M= [5,4,3,2,1]r. Montrer que le nombre entier N−Mest divisible par 16.
Réponse.
M= 5r4+ 4r3+ 3r2+ 2r+ 1 ≡16 5b4+ 4b3+ 3b2+ 2b+ 1 = N
parce que r≡16 bet donc aussi r2≡16 b2et 3r2≡16 3b2, etcetera.DoncN-M≡16 0, c.-à-d. 16|(N−
M).
3a) [4 pts] Montrer par induction que pour chaque nombre entier n≥4on a
n−1
X
r=3
r(r!) = n!−6.
(Remarque : Il faut surtout bien rédiger votre preuve selon le modèle utilisé en classe.)
Réponse. Posons pour n≥4la proposition logique
P(n) := ”
n−1
X
r=3
r(r!) = n!−6”.
Il faut montrer par induction que P(n)est vraie pour chaque nombre naturel n≥4.
Début : P(4) = ”3(3!) = 4! −6” est vraie parce que en effet 3(3!) = 18 = 4! −6.
Étape d’induction. Soit n≥4et supposons P(n)vraie, c.-à-d. Pn−1
r=3 r(r!) = n!−6. Ajoutons
aux deux côtés n(n!), alors Pn−1
r=3 r(r!) + n(n!) = n!−6 + n(n!). La partie gauche de l’équation est
P(n+1)−1
r=3 r(r!) ; la partie droite de l’équation on peut réécrire comme
n!−6 + n(n!) = (n+ 1)n!−6=(n+ 1)! −6.
On obtient P(n+1)−1
r=3 r(r!) = (n+ 1)! −6, et P(n+ 1) est vraie. C.-à-d., nous avons montré que
P(n)→P(n+ 1) est vraie.
Conclusion : nous avons montré par induction que P(n)vraie pour n≥4. Et c’est ça ce qu’il
fallait montrer.

3
3b) On a montré dans le cours que pour chaque entier n≥2il existe un unique nombre naturel
s=s(n)et aussi snombres premiers tels que n=p1p2· · · ps. Acceptons ça.
(i) [2 pts] Donner s(6), s(20), s(120) et montrer qu’on a
s(nm) = s(n) + s(m)
pour chaque n≥2et m≥2.
(ii) [3 pts] Montrer par induction généreuse sur n∈Nque pour chaque nombre entier impair
n≥3on a 1
n≤(1 3)s(n).
(Remarque : En particulier, une preuve directe ne sera pas acceptée ici.)
Réponse. (i) 6=2·3alors s(6) = 2 ;20 = 2·2·5alors s(20) = 3,120 = 2·2·2·3·5, alors s(120) = 5.
Si n=p1· · · pset m=q1· · · qt, avec les piet qjdes premiers, alors nm =p1· · · ps·q1· · · qtest un
produit de s+tpremiers, alors s(nm) = s(n) + s(m).
(ii) Posons pour chaque n≥2la proposition logique P(n) :="Si nest impair alors 1
n≤(1 3)s(n)".
À montrer par induction généreuse que P(n)vraie pour chaque entier n≥2.
Début : P(2) est vraie : parce que 2est pair alors l’implication P(2) est automatiquement vraie
(l’hypothèse de l’implication P(2) est fausse).
Étape d’induction. Soit n≥2. Supposons P(k)vraie pour chaque 2≤k≤n. À montrer que
P(n+ 1) est vraie aussi.
Si n+ 1 est premier, alors s(n+ 1) = 1,n+ 1 ≥3et n+ 1 est impair (car n+ 1 6= 2). Donc en
effet 1
n+1 ≤(1 3)s(n+1) =1 3. Dans ce cas l’implication P(n+ 1) est vrai.
Si n+ 1 est pair, alors P(n+ 1) est automatiquement vrai (parce que l’hypothèse de cette
implication est fausse).
Si n+ 1 ≥3est impair, mais pas premier, alors n+ 1 = ab, où 2≤a≤net 2≤b≤n. Parce que
n+ 1 est impair, nécessairement aet bsont impairs aussi. L’hypothèse d’induction s’applique pour
aet b, alors P(a)et P(b)sont vraies. Parce que aet bsont impairs, ça implique que 1
a≤(1 3)s(a)et
1
b≤(1 3)s(b).
On a s(n+ 1) = s(a) + s(b)(par (i)) donc 1
n+1 =1 a·1 b≤(1 3)s(a)·(1 3)s(b)= (1 3)s(n+1). Alors
P(n+ 1) est vrai aussi.
Conclusion : par induction P(n)est vraie pour chaque n≥0.