Mouvement de rotation, approche énergétique eh C −= θ

Sup PCSI1 - Exercices de physique mouvement de rotation, approche énergétique.
1
Mouvement de rotation, approche énergétique
1. Mouvement d'un cylindre :
a) Un cylindre peut tourner librement autour de son axe
horizontal ∆ qui est fixe par rapport au référentiel du
laboratoire considéré comme galiléen. Le moment
d'inertie du cylindre par rapport à ∆ est J ; son rayon
est R.
Un fil inextensible et de masse négligeable est enroulé
autour du cylindre ; un corps de masse m est attaché à
l'extrémité libre de ce fil.
Caractériser le mouvement de m que l'on pourra repérer par la coordonnée z comptée suivant la verticale
descendante et décrire l’évolution ω(t) de la vitesse angulaire du cylindre. On souhaite traiter la question par
une méthode énergétique.
b) Le dispositif précédent est modifié : un système de
palettes est fixé sur l’axe; l’entraînement en rotation
de ces palettes introduit un couple de frottement
fluide dont le moment, de module M
f
= hߠሶ s’oppose
au mouvement. Déterminer l’évolution temporelle de
la vitesse angulaire ω(t) du cylindre, partant d’une
valeur initiale nulle. (Le fil est supposé suffisamment
long pour ne pas arriver en bout de déroulement avant
la fin de l’étude...)
Réponses :
a) écrire la conservation de l’énergie pour le système (cylindre, masse suspendue), en faisant intervenir
l’énergie cinétique de rotation du cylindre autour de l’axe ∆, l’énergie cinétique de la masse suspendue et
son énergie potentielle de pesanteur. Par la présence du fil ݖሶ = ܴ ߠሶ
On peut aussi écrire la variation de l’énergie cinétique du cylindre comme égale à la puissance
développée par la tension du fil ; cette tension étant explicitée à partir de la RFD écrite pour la masse m
ou par un bilan énergétique instantané pour la masse m.
ω(t) = mgR.t / (J + mR²).
b) Dans le bilan énergétique précédent, vient s’ajouter la puissance dissipée par frottement fluide -hߠሶ².
ω(t) = (mgR / h).(1 – exp(-t/τ)) avec τ = h / (J + mR²).
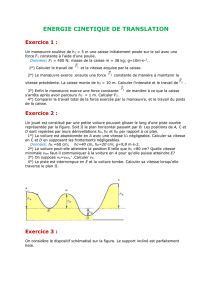
2. Pendule avec frottement :
Un dispositif est constitué d’une barre de masse négligeable, de
longueur 3a, portant à ses extrémités des masses m et 2m, assimilables
à des points matériels, pouvant tourner dans un plan vertical autour
d’un axe horizontal passant à une distance 2a de la masse 2m.
Le pendule est lâché sans vitesse initiale, avec un angle θ = θ
o
. La liaison
pivot est supposée non idéale : le mobile subit un frottement linéaire
traduit par un couple de frottement de moment :
x
ehC
•
−= θ
. Etablir
l’équation du mouvement à partir d’un bilan énergétique.
Etudier θ(t) si θ
o
est proche de π, et en considérant h faible.
θ
g
2a
2m
m
a
y
z

Sup PCSI1 - Exercices de physique mouvement de rotation, approche énergétique.
2
Réponse : voir exercice sur la même situation dans feuilles d’exercice « Lois du moment cinétique ».
3. Mise en mouvement d'un volant par un rotor :
Un rotor constitué d’un solide S
1
et un volant d’inertie S
2
peuvent tourner sans frottement autour d'un axe de
rotation horizontal (zz') commun. S
1
tourne à la vitesse angulaire ω
o
, et S
2
est initialement immobile. On désigne
respectivement par J
1
et J
2
les moments d'inertie de S
1
et S
2
par rapport à l'axe (zz').
La mise en rotation de S
2
à partir du mouvement de S
1
est
obtenue par un système d’embrayage. A un instant donné, on
met en contact les deux disques D
1
et D
2
solidaires
respectivement de S
1
et S
2
. Ces disques ont un moment
d’inertie négligeable.
Au bout d'un certain temps, du fait des frottements entre D
1
et D
2
, le rotor et le volant tournent à la même vitesse ω
f
.
1°) Déterminer la vitesse angulaire ω
f
.
2°) Faire un bilan énergétique entre l'état initial et l'état final du système et exprimer le travail des forces de
frottement.
Réponses :
1°) Ecrire le TMC. Conservation du moment cinétique, donc J
1
.ω
o
= (J
1
+ J
2
).ω
f
2°) W
frott
= ∆E
c
= ... = J
1
.J
2
.ω
o
/ (2.(J
1
+ J
2
))
4. Contraction d’un système d’étoile double :
Un système d’étoile double est constitué de deux étoiles E
1
et E
2
de masses respectives m
1
et m
2
en interaction
gravitationnelle. Toute interaction avec d’autres astres est supposée négligeable. L’ensemble constitue un
système lié.
A l’état initial, les deux étoiles tournent autour de leur barycentre G, à une distance respective d = E
1
E
2
et avec
une vitesse angulaire Ω, selon des trajectoires circulaires de centre G. Du fait de phénomènes dissipatifs,
mettant en jeu une perte énergétique W, les deux étoiles sont amenées progressivement à se rapprocher l’une
de l’autre à une distance d’ = E
1
E
2
. On suppose qu’elles conservent pratiquement une trajectoire circulaire
durant le processus, le rayon de cette trajectoire variant à mesure que leur distance passe de d à d’.
Faire un bilan énergétique du processus. Calculer la valeur que prendra alors la période de révolution des étoiles
autour de leur barycentre. On notera K = 6,67.10
-11
usi.
Réponse : Bilan énergétique : ∆ E = -W = ∆ E
c
+ ∆ E
p
; T’ =2 π / Ω ’
avec
( ) ( )
(
)
21
21
2
21
.
2.
1
'
1
2
'
1
'mm
mm
Wd
dd
mmK
d
+
−Ω+
−+=Ω
S
1
D
1
D
2
S
2