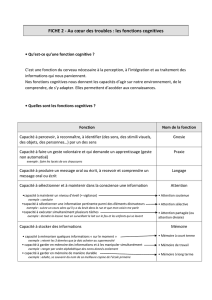
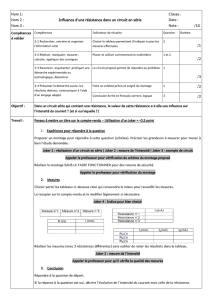
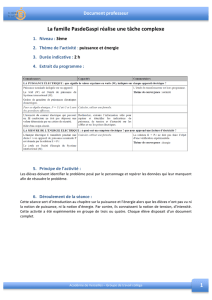
Histoires détectives

Sciences Cognitives – Université de Mons-Hainaut
2004
Histoires détectives
Degré moyen
C. VANDEPUTTE et M. MEUNIER

Sciences Cognitives – U.M.H.
2004
2
Introduction
Au début des années 70, Frédérique écrit les premières « histoires détectives » dans
le cadre de ses activités de recherche au C.S.M.P.
Toutes ces histoires détectives sont basées sur le même principe : des indices
successifs permettent de découvrir un nombre. Mais parfois, il est judicieux
d’exploiter les indices dans un ordre différent de l’ordre dans lequel ils sont
présentés !
Nous nous sommes inspirés des idées de Frédérique pour réaliser le présent
fascicule. Sur chaque page vous trouverez une histoire détective. Ces histoires sont
accessibles aux enfants dès la troisième primaire
∗
.
T OUS LES NOMBRES SECRETS DE CE FASCICULE SONT DES NATURELS .
La plupart des indices utilisent des outils avec lesquels les enfants sont familiarisés.
Toutefois un des outils pourrait être inconnu : le minicomputer de Papy. Il s’agit d’un
abaque qui combine les avantages du binaire et du décimal. Les plaques se
succèdent selon les règles des abaques classiques (unités, dizaines, centaines, …)
mais chaque plaque est divisée en 4 carrés. Les nombres s’écrivent à l’aide de pions
ou de jetons, selon les règles ci-dessous :
Par conséquent,
représente le nombre 7655
Afin d’aider les élèves à mémoriser la valeur de chaque case, les plaques peuvent
être coloriées en utilisant les couleurs des réglettes Cuisenaire correspondant à leur
valeur :
Seules deux plaques du minicomputer (celle des unités et celle des dizaines) sont
utilisées dans ce fascicule.
Néanmoins toutes les histoires où figure un indice utilisant le minicomputer ont été
« traduites » en histoires sans minicomputer. (exemple : l’histoire n°1)
∗
Il n’est pas nécessaire de connaître les formules de l’aire du triangle et du parallélogramme pour
résoudre les histoires 4, 5, 6. Une utilisation judicieuse du quadrillage est suffisante. Des jokers sont
fournis en ce sens. Ces histoires permettent d’ailleurs de préparer la découverte des formules en
question.

Sciences Cognitives – U.M.H.
2004
3
Vous avez donc le choix entre :
• introduire brièvement le minicomputer de Papy. Dans ce cas, il serait bon que
les élèves disposent de plaques individuelles : des pions et deux carrés
divisés en quatre, dessinés chacun sur une feuille suffisent.
ou
• remplacer les histoires 1, 2, 3 et 9 par les histoires 1’, 2’, 3’ et 9’.
Afin de permettre l’accès autonome d’un maximum d’enfants à ces histoires, nous
avons essayé de présenter la plupart des indices de manière aussi peu verbale que
possible. Des jokers sont fournis en pages 18, 19, 20 et 21.
Certains « traduisent » les indices présentés de manière plus verbale. N’hésitez pas
à les découper et à les coller à la place indiquée pour les élèves qui n’auraient pas
atteint le niveau de lecture requis. D’autres servent simplement d’aide pour résoudre
les exercices.
N’hésitez pas non plus à créer vos propres histoires détectives, adaptées à la
progression de vos élèves… ou à demander à ceux-ci de créer des histoires à
résoudre par leurs condisciples.
Bon amusement !

Sciences Cognitives – U.M.H.
2004
4
TOUS LES NOMBRES UTILISES
DANS CE FASCICULE SONT
DES NOMBRES ENTIERS

Sciences Cognitives – U.M.H.
2004
5
Histoire 1
KWAT est un nombre secret.
Indice 1 : KWAT est sur ce diagramme fléché.
KWAT peut être :
Indice 2 : KWAT est un carré
c’est-à-dire KWAT = x
KWAT peut être :
Indice 3 : KWAT peut s’écrire en plaçant exactement 2 pions sur des
cases différentes des 2 premières plaques du minicomputer
(joker 1 page 18).
KWAT est :