4 Continuité d`une fonction

1
CONTINUITE D’UNE FONCTION
Soit f une fonction et I un intervalle inclus dans D
f
.
I- Continuité d’une fonction
1) Continuité d’une fonction en un point, sur un intervalle
Définitions : • Dire que f est continue en un point a de I signifie que :
ax
lim
→f (x) = f (a)
• Dire que f est continue sur I signifie que f est continue en tout point de I.
Interprétation graphique : Si f est continue, alors C
f
est tracée en un seul morceau.
f est continue f (x) = E (x) f n’est pas continue
Conséquence : D’après la définition et les théorèmes d’opérations sur les limites, la somme,
le produit, la composée de fonction continues sont continues.
2) Dérivabilité et continuité
Théorème : • Si f est dérivable en un point a de I, alors f est continue en a.
• Si f est dérivable sur I, alors f est continue sur I.
Démonstration (BAC) :
f est dérivable en a ⇔ ax
lim
→
(
)
(
)
ax afxf −
−
= f’(a) Posons : g (x) =
(
)
(
)
ax afxf −
−
.
(x – a) g (x) = f (x) – f (a) ⇔ f (x) = f (a) + (x – a) g (x)
ax
lim
→g (x) = f’(a) et ax
lim
→(x – a) = 0 ⇒ ax
lim
→f (x) = f (a)
Remarques : • La réciproque est fausse. Une fonction peut être continue en un point sans être
dérivable en ce point.
Contre-exemple : Soit f : x ï | x |. 0x
lim
→f (x) = 0 = f (0) donc f est continue en 0.

2
(
)
(
)
x
x
0x 0fxf = −
−
x
x
lim
0x
+
→
=
x
x
lim
0x + →= 1
x
x
lim
0x − → =
x
x
lim
0x
−
+
→= - 1.
En 0, f admet une dérivée à droite et une dérivée à
gauche, mais elles ne sont pas égales. Donc f n’est pas
dérivable en 0.
• Si f n’est pas continue, alors f n’est pas dérivable.
3) Conséquences : • f : x ï x est continue sur
*
IR
+
.
• Les fonctions polynômes sont continues sur car dérivables sur .
• Les fonctions rationnelles sont continues sur tout intervalle contenu dans leur ensemble de
définition.
• Les fonctions sinus et cosinus sont continues sur .
• Toutes les fonctions construites algébriquement par somme, produit, quotient, composition
de fonctions usuelles sont continues sur tout intervalle contenu dans leur ensemble de défini-
tion.
II- Fonctions continues et résolution d’équations
Posons I = [a, b], avec a < b.
1) Théorème des valeurs intermédiaires
Théorème : Soit f une fonction continue sur [a, b]. Alors, pour tout réel y compris entre f (a)
et f (b), il existe au moins un réel c compris entre a et b tel que : f (c) = y .
Supposons f (a) ≤ f (b). Le théorème signifie que :
• Pour tout y de [f (a), f (b)], l’équation f (x) = y a au moins une solution dans I.
• Tout réel y de [f (a), f (b)] est l’image par f d’au moins un réel c de I. c n’est pas unique.
Démonstration en travaux dirigés.
a c b
f (a)
y
f (b)

3
2) Fonction continue, strictement monotone sur [a, b]
Théorème : Si f est continue, strictement croissante sur I, alors :
1) L’image de I par f est [f (a), f (b)].
2) Pour tout réel y de [f (a), f (b)], l’équation f (x) = y a une solution unique dans I.
Démonstration ( BAC) : 1) Montrons que f (I) = [f (a), f (b)].
• Soit x dans I : f (x) ∈ f (I).
a ≤ x ≤ b et f strictement croissante sur I ⇒ f (a) ≤ f (x) ≤ f (b) ⇒ f (x) ∈ [f (a), f (b)]
D’où : f (I) ⊂ [f (a), f (b)].
• Soit y dans [f (a), f (b)]. D’après le théorème des valeurs intermédiaires, y est l’image d’au
moins un réel c de I. Donc : y ∈ f (I). D’où : [f (a), f (b)] ⊂ f (I).
Donc : f (I) = [f (a), f (b)].
2) Unicité de la solution: L’équation f (x) = y ne peut pas avoir deux solutions car, f étant
strictement croissante, 2 réels distincts ont des images distinctes.
Cas particulier : Si f est continue et strictement monotone sur I, et si f (a) f (b) < 0, alors
l’équation f (x) = 0 a une solution unique dans I.
Démonstration : f (a) f (b) < 0 ⇒ f (a) ≠ 0 et f (b) ≠ 0 et f (a) et f (b) de signes contraires.
Donc : 0 ∈ [f (a), f (b)] si f est croissante ou 0 ∈ [f (b), f (a)] si f est décroissante.
Remarques :
2
2
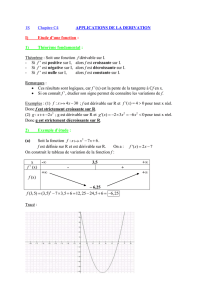
Exemple : Soit f : x ï x
3
– 3x² - 1.
Démontrer que l’équation f (x) = 0 admet une solution unique α dans [2, 4]. Donner un enca-
drement de α d’amplitude 10
- 2
.
f’(x) = 3x² - 6x = 3x (x – 2) f’(x) = 0 ⇔ 3x (x – 2) = 0 ⇔ x = 0 ou x = 2
Sur [2, 4], f est continue car elle est dérivable. Elle est strictement croissante. Donc l’équation
f (x) = 0 a une solution unique.
•
L’existence de la solution de l’équation f (x) = y vient du
fait que f est continue.
Si f n’est pas continue, alors l’équation f (x) = c n’a pas de
solution.
Dans l’exemple ci-contre, l’équation f (x) = 2 n’a pas de
solution.
•
L’unicité de la solution de l’équation f (x) = y vient du
fait que f est strictement monotone.
Dans l’exemple ci-contre, l’équation f (x) = 2 a une infinité
de solutions.
x
f'(x)
)
f (x )
− ∞
+
−
∞
0
−
− 1
2
+
+ ∞
+ ∞
- 4

4
A la calculatrice : f (3,1) = - 0,039 et f (3,2) = 1,048.
f (3,11) = 0,06393 donc : α ∈ ] 3,1 ; 3,11 [.
4) Extension du théorème précédent
Lorsque f est continue et strictement monotone, le théorème précédent s’étend à un intervalle
I quelconque.
Exemple : Démontrer que l’équation ( E ) : x x = 1 – x a une solution unique sur 
+
.
( E ) ⇔ x x + x = 1 ⇔ f (x) = 1 avec f : x ï x x + x .
f est dérivable comme somme et produit de fonctions dérivables donc f est continue.
f’(x) = x + x2
x+ 1 =
2
x3 + 1 Sur
+
, f’(x) > 0, donc f est strictement croissante.
f ( [0, + ∝ [ ) = [ f (0), ∞+→x
lim
f (x) [ = [0, + ∝ [.
1 ∈ [0, + ∝ [. D’après le théorème des valeurs intermédiaires, il existe α dans [0, + ∝ [ tel que :
f ( α ) = 0.
5) Notion de fonction réciproque
Soit f continue et strictement monotone sur I. Posons f (I) = J.
• Pour tout x de I, f (x) ∈ J.
• Pour tout y de J, il existe x unique dans I tel que y = f (x).
Lorsque ces deux conditions sont réunies, on dit que f est une bijection de I sur J .
On peut définir une fonction g sur J : y ï x telle que :
y = f (x) ⇔ x = g (y).
g est la fonction réciproque de f . On la note f
– 1
.
y = f (x) ⇔ x =
(
)
yf
1−
On a :
Pour tout x de I,
(
)
[
]
(
)
yfxff
11 −−
= = x.
Pour tout y de J,
(
)
[
]
yff
1−
= f (x) = y.
x = g (y)
y = f (x)