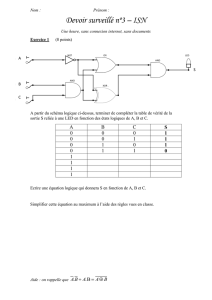
Algèbre et géométrie

CM(z)
M z ∈C
z∈C
z3−8z2+ 24z−32 = 0.
z0= 4
a, b, c z3−8z2+ 24z−32 = (z−4)(az2+bz +c)
az3+(b−4a)z2+(c−4b)z−4c
a= 1
b−4a=−8c−4b= 24 4c= 32 a= 1 b=−4c= 8
(E)
(E)⇐⇒ (z−4)(z2−4z+ 8) = 0
z(E)z−4=0 z2−4z+ 8 = 0
z2−4z+ 8 = 0 ∆ = 16 −4×8 = −16 = (4i)2
z1= 2 + 2i z2= 2 −2i.
(E){z0, z1, z2}
z1z2
|z1|=|z2|= 2√2
z1= 2√2(√2
2+i√2 2)=2√2 eiπ
4z2= 2√2(√2
2−i√2 2)=2√2 e−iπ
4
M0(z0)M1(z1)M2(z2) Ω
ω= 2 R= 2
|z0−ω|=|4−2|= 2 |z1−ω|=|2i|= 2 |z2−ω|=| − 2i|= 2
M0M1M22 Ω
z|z|= 1 z6= 1 iz+ 1
z−1∈R
Z=iz+1
z−1Z=Z|z|= 1 z6= 1
Z=−iz+ 1
z−1=−i(z+ 1)z (z−1)z=−i1 + z 1−z=Z.
z|z|= 1 z6= 1 1
1−z=1 2

Z=1
1−z2 (Z) = Z+Z= 1
1
1−z+1 1−z=1−z+ 1 −z (1 −z)(1 −z)=2−(z+z) 1−z−z+zz =2−(z+z) 2−(z+z)= 1,
zz = 1
Cz3=z
z|z3|=|z|3=|z|=|z| |z|3=|z|
|z|(|z|2−1) = |z|(|z| − 1)(|z|+ 1) = 0 |z|= 0
|z|= 1 0 |z|= 1
∀z∈C|z|= 1
z3=z⇐⇒ z4=zz = 1
⇐⇒ z4= 1
⇐⇒ z∈U4.
S={0} ∪ U4={0,1,−1, i, −i}
(S)
x−2y+ 3z= 5
2x−4y+z= 5
3x−5y+ 2z= 8
(S)⇐⇒ 
x−2y+ 3z= 5
2x−4y+z= 5
3x−5y+ 2z= 8
⇐⇒ 
x−2y+ 3z= 5
−5z=−52←2−21
y−7z=−73←3−31
⇐⇒ 
x−2y+ 3z= 5
y−7z=−7 ( 2↔3)
−5z=−5
0
(S)⇐⇒ 
x−2y+ 3 = 5
y−7 = −7
z= 1
⇐⇒ x−2y= 2
y= 0 z= 1.
⇐⇒ x= 2, y = 0, z = 1.
S={(2,0,1)}
a, b ∈R
(Sa,b)
x−y+z= 1
−ax +ay −z= 5
bz = 1
S(Sa,b)

aS
a= 0 b= 1 z=−5z= 1
b6= 0 aS
(a, b)6= (1,1) S
(Sa,b)⇐⇒ 
x−y+z= 1
(a−1)z= 5 + a2←2+a1
bz = 1
(a, b)6= (1,1) (a−1)
y z
(Sa,b)⇐⇒ 
x+z−y= 1
(a−1)z= 5 + a
0 = 1 −b(5+a)
a−1
a6=−5S 6=∅ ⇐⇒ b=a−1
a+5
y
(0,0,1) ∈ S b= 1