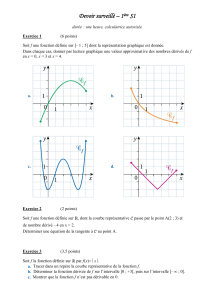
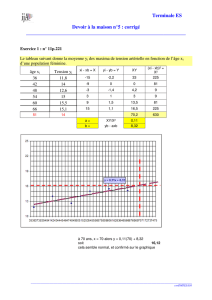
Corrigé du devoir n°1

Solutions du devoir n˚1 page 1 de 2
Solutions du devoir n˚1
I) Vrai ou faux ?
1. « Dire que √3x2+ 1 + 2x= 0 équivaut à dire que x2= 1 »
Faux .
L’implication « √3x2+ 1 + 2x= 0 implique x2= 1 » est vraie mais la réciproque
est fausse : le nombre 1 vérifie x2= 1 mais il ne vérifie pas √3x2+ 1 + 2x= 0
(puisque √3 + 1 + 2 = 4)
Le problème vient du passage de √3x2+ 1 = −2xà3x2+ 1 = (−2x)2.
En élevant au carré, on obtient toujours une implication (a=b⇒a2=b2), mais
on n’obtient une équivalence que si les deux membres sont de même signe.
Pour démontrer qu’une équivalence est fausse il suffit d’un contre-exemple qui
montre que l’une des deux propriétés peut être vraie alors que l’autre ne l’est pas.
2. « Dire que −36x63équivaut à dire que −16x3−12x+ 8 617 »
Faux .
On a bien f(−3) = 17 et f(3) = −1, mais fn’est pas monotone, elle change de
sens et elle dépasse ces valeurs.
Il suffit d’un contre-exemple : f(2) = −8, qui n’est pas compris entre −1et 17.
−3
32
Cela montre que a6x6bn’implique pas nécessairement f(a)6f(x)6f(b)ni
même f(b)6f(x)6f(a). Cela dépend du sens de variation de f.
3. « Dire qu’une fonction définie sur Rne s’annule jamais équivaut à dire qu’elle garde
un signe constant »
Faux .
Le problème est le suivant : la fonction est-elle continue ? (concept et théorème à
voir plus tard).
Contre-exemple : f(x) = −1pour x < 0et f(x)=1pour x>0.
•
fne s’annule pas mais ne garde pas un signe constant.
Cependant la réciproque est vraie : si fgarde un signe constant (au sens strict),
alors elle ne s’annule pas (par définition elle est toujours ou bien strictement positive
ou bien toujours strictement négative, donc jamais nulle).
II) Rédaction
Attention : décroissante n’est pas le contraire de croissante.
1. a) « La fonction fn’est pas croissante sur R» se traduit par :
Il existe aet bréels tels que a<bet f(a)> f(b).
(il suffit qu’il existe deux nombres de ce type)
Cette phrase traduit le contraire de :
Pour tout aet bdans R, si a < b, alors f(a)6f(b).
Notez que le contraire de f(a)6f(b)est f(a)> f(b)
Exemple : f(x) = −x.
0<1mais f(0) > f(1) car f(0) = 0 et f(1) = −1.
b) « La fonction fn’est pas strictement croissante sur R» se traduit par :
il existe aet bréels tels que a<bet f(a)>f(b).
(il suffit qu’il existe deux nombres de ce type).
Remarquez la légère différence avec la propriété précédente.
Exemple : f(x)=0.
0<1mais f(0) >f(1) car f(0) = 0 = f(1).
c) « La fonction fn’est pas constante sur R» se traduit par :
il existe aet bréels tels que a6=bet f(a)6=f(b).

Solutions du devoir n˚1 page 2 de 2
Exemple : f(x) = x,a= 0 et b= 1
2. Soit fla fonction définie par f(x) = x2√2−4√2x
x−∞ 0 1 +∞
f0(x)−0+
f(x)
0
−3√2
+∞
– la fonction fest définie sur [0; +∞[.
En effet, la condition de définition est 2x>0
– la fonction fest dérivable sur ]0; +∞[
Sur ]0; +∞[, on peut appliquer les théorèmes sur les opérations et les composi-
tions de fonctions usuelles (car 2x > 0, on peut donc composer avec la racine
carrée).
En 0 : il faut calculer le taux d’accroissement t(x) = x2√2−√2x
x.
La limite se présente (comme toujours) sous la forme indéterminée « 0
0»
On lève l’indétermination en simplifiant par √x:t(x) = x√x√2−√2
√x.
Le numérateur tend vers −√2et le dénominateur tend vers 0 en restant positif,
donc la limite est −∞. Ce n’est pas un réel, donc fn’est pas dérivable en 0.
Donc le domaine de dérivabilité est ]0; +∞[
– signe de f0:f0est strictement négative sur ]0; 1[, nulle en 1 et strictement positive
sur ]1; +∞[.
Pour prouver cela, on calcule f0(x)=2x√2−42
2√2x=··· =4(x√x−1)
√2x
Quand a-t-on f0(x)>0(par exemple) ?
Quand x√x > 1, ce qui est équivalent à x3>1(on élève au carré, ce qui donne
une équivalence car les deux membres sont positifs).
Cela équivaut à x > 1car la fonction cube est strictement croissante.
On en déduit le signe de f0(x).
Notez qu’il faut résoudre une inéquation f0(x)>0et pas une équation f0(x)=0.
– sens de variation de f:
fest strictement décroissante sur ]0; 1[ et strictement croissante sur ]1; +∞[.
– valeurs et limites : f(0) = 0 et f(1) = −3√2
La limite de fen +∞est +∞
La forme donnée pour fest indéterminée lorsque xtend vers +∞(« ∞−∞»)
On lève l’indétermination en factorisant : f(x) = √x(x√x√2−4√2).
Le forme n’est plus indéterminée (« ∞×∞»). La limite est donc +∞.
III) Recherche
Dans une stricte démonstration mathématique, il suffit de donner les formules solutions
et de vérifier qu’elles sont solutions (et de démontrer qu’elles sont uniques).
Mais ce n’est pas l’objectif de l’exercice, qui demande de "raconter" la recherche effec-
tuée.
On peut par exemple procéder par recherche de conditions nécessaires puis démontrer
qu’elles sont suffisantes.
1. Conditions nécessaires et unicité
Si vraiment il existe uet vsolutions (avec upaire et vimpaire), alors on doit avoir
f(x) = u(x) + v(x)et f(−x) = u(−x) + v(−x) = u(x)−v(x).
On peut alors considérer ces relations comme un système d’équations avec uet v
comme inconnues :
f(x) = u(x) + v(x)
f(−x) = u(x)−v(x)
On résout ce système en faisant la somme et la différencer des équations :
f(x) + f(−x)=2u(x)
f(x)−f(−x)=2v(x).
Donc u(x) = f(x) + f(−x)
2et v(x) = f(x)−f(−x) 2.
Cela prouve qu’il ne peut pas y avoir d’autres solutions, mais cela ne prouve pas
encore que ce sont bien des solutions au problème initial.
2. Conditions suffisantes et existence
Il faut maintenant démontrer que les fonctions get hdéfinies par
g(x) = f(x) + f(−x)
2et h(x) = f(x)−f(−x) 2sont bien respectivement paires et
impaires et que f(x) = g(x) + h(x)
g(−x) = f(−x) + f(x)
2. C’est bien égal à g(x).
h(−x) = f(−x)−f(x)
2. C’est bien égal à −h(x).
D’autre part g(x) + h(x) = f(x) + f(−x) + f(x)−f(−x)
2=f(x).
Donc on a bien prouvé l’existence et l’unicité cherchées, pour toute fonction f.
3. Exemple f(x) = 1
x2+x+ 1
Le calcul avec les formules précédentes donne :
g(x) = x2+ 1
(1 + x+x2)(1 −x+x2)et h(x) = −x (1 + x+x2)(1 −x+x2)