Fiche élève DEVOIR MAISON N°4 word

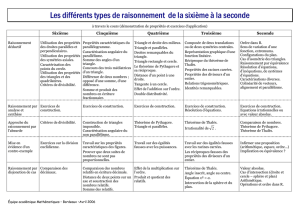
Exemple de progression en classe de seconde Équipe Académique Mathématiques
Bordeaux
DEVOIR MAISON N°4
Exercice 1
Sur la figure ci-dessous, les trois cercles c1, c2 et c3 de centres respectifs I, O et J, ont le même rayon, qui est
un entier naturel x. La droite (NM) est tangente au cercle c3 en M et coupe c2 en A et B.
On pose OH = a et AB = b.
1) Calcul de a
a) A l’aide du théorème de Thalès, exprimer a en fonction de x.
b) Quelle est la nature du nombre a ?
c) Quelles sont les valeurs de x pour lesquelles a est un nombre entier ?
2) Calcul de b
a) A l’aide du théorème de Pythagore, exprimer HB, puis b en fonction de x.
b) Quelle est la nature du nombre b ?
c) Quelles sont les valeurs de x pour lesquelles b est un entier ?
3) Réaliser la figure pour x = 5 cm.
Exercice 2
VRAI ou FAUX ? Justifier la réponse.
 Pour tout réel x , les deux nombres 2(x + 1)(x – 3) et (2 x + 2)( 2 x – 6) sont égaux.
 Pour tout réel x ,
9 3
2
x + = x+
.
 La somme de trois nombres entiers consécutifs est divisible par 3.
 Le carré de tout nombre réel est supérieur ou égal à ce nombre.