Thermodynamique et processus des réactions redox

THERMODYNAMIQUE ET CINÉTIQUE DES PROCESSUS REDOX 1
I-E NTHALPIE LIBRE DES RÉACTIONS REDOX , USAGES 1
1-R APPEL : ÉTUDE DES PILES 1
2-E NTHALPIE LIBRE D ’ UNE RÉACTION REDOX ASSOCIÉE À UNE PILE 2
2-a- échange d’énergie électrique 2
2-b- Variation élémentaire d’enthalpie libre du système redox 3
2-c- Enthalpie libre de réaction redox 3
3-E NTHALPIE LIBRE STANDARD D ’ UNE DEMI - ÉQUATION REDOX 5
4-R ÉSUMÉ : A PPLICATIONS PRATIQUES 5
Constante d’équilibre 5
Sens de réaction 5
Calculs de potentiels standards 5
II.E TUDE DE LA CINÉTIQUE DES REACTIONS REDOX 7
1-P RÉVISIONS THERMODYNAMIQUES ET RÉALITÉS CINÉTIQUES 7
1-a- La prévision thermodynamique : exemples de l’oxydation et de la réduction de l’eau 7
1-b- La méthode expérimentale de tracé : le montage à 3 électrodes 9
1-c- Réalités expérimentales : surtensions et courants limites de diffusion 9
1-d- Passivation d’un métal 12
2- E XPLOITATION DES COURBES I/E : ÉLECTROLYSE , GÉNÉRATEURS , RÉACTIONS SPONTANÉES 13
2-a- Electrolyses 13
2-b- Générateurs : Piles et accumulateurs 21

Thermo et cinétique des processus redox 1
THERMODYNAMIQUE ET CINÉTIQUE DES PROCESSUS REDOX
I-ENTHALPIE LIBRE DES RÉACTIONS REDOX, USAGES
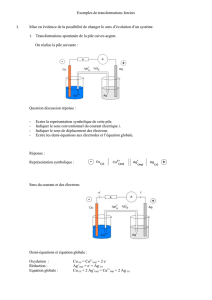
1-Rappel : étude des piles
V
Ox
1
+ red
1
Red
2
+ ox
2
pH
1
pH
2
Réaction redox conventionnelle associée à la pile :
ox
2
+ red
1
= red
2
+ ox
1
(l’ordre des réducteurs est le même que dans le schéma de la pile )
Question : Dans quel sens a lieu cette réaction si l’on
ferme l’interrupteur ?
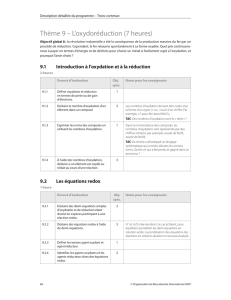
e
-
e
-
V
+ -
Ox
1
+ e
-
 red
1
Red
2
 ox
2
+ e
-
(cathode) (anode)
Donc la réaction de fonctionnement de la pile est :
ox
1
+ red
2
 ox
2
+ red
1
ox
1
red
1
x
E(1) M(1) (zone)
x
ox
2
x M(2) ( zone)
E(2) red
2
x
pH
E
gauche
(1) > E
droite
(2)  + en (1) et – en (2)
=> E
pile
= E
droite
(2) - E
gauche
(1) < 0
Rappel : un mélange d’un oxydant et d’un réducteur
est modélisable par une pile en court circuit .
Conclusion : Un oxydant et un réducteur n’ayant pas
de domaine commun réagissent quasi-
quantitativement . Si au contraire un oxydant et un
réducteur ont un domaine commun , ils coexistent
(presque) sans réaction.
Exercice :
On réalise la pile suivante : Ag / Ag
+
( 0,1 mol.L
-1
) // Ni
2+
( 0,001 mol.L
-1
) /Ni.
1. Décrire en s'aidant d'un schéma annoté la réalisation d'une telle pile.
2. Déterminer la polarité de la pile et sa f.e.m. Écrire les équations des réactions se produisant à chaque
électrode ainsi que la réaction bilan du fonctionnement de la pile.
3. Quelle est la variation de masse de l'électrode constituant le pôle négatif de la pile lorsque celle-ci débite un
courant d'intensité constante I=10mA pendant 3 heures ? Quelle est la variation de concentration de la
solution ( 100 mL) d'ions argent dans le même temps ?
4. Donner les valeurs minimales en nbe de moles d'Ag
+
et en masse de nickel pour assurer une capacité à cette
pile de 2800 mA.h .
Potentiels standard: E
o
(Ag
+
/Ag) = 0,80V ; E
o
(Ni
2+
/Ni) = -0,23V.
Masses molaires atomiques: M(Ag) = 107,9g.mol
-1
; M(Ni) = 58,7g.mol
-1
;

Thermo et cinétique des processus redox 2
2-Enthalpie libre d’une réaction redox associée à une pile
La connaissance du potentiel d'une pile permet de déduire le sens de la réaction associée, de même que la
connaissance du signe de A = − ∆
r
G ( ≠ - ∆
r
G° ) permet de connaître le sens d'évolution du système chimique étudié.
Il doit être possible de relier la ddp E et ∆
r
G.
2- A - ÉCHANGE D ’ ÉNERGIE ÉLECTRIQUE
Ce sont les électrons qui sont les vecteurs de l’énergie pour un système redox.
L’énergie potentielle d’une charge q, placée à un potentiel Φ vaut : E
p
= qΦ
On définit la fem e ( force électromotrice d’une pile ) comme la valeur absolue de la ddp à ses bornes, soit e = E
+
- E
-
Envisageons les 2 cas possibles pour les systèmes redox : fonctionnement en pile ou en électrolyse :
+ -
+ -
Pendant un temps dt, dn électrons sortent du système, pendant que dn y rentrent. On peut donc considérer que le
système est fermé, avec un changement d’énergie pour ces dn électrons du système. La charge de ces dn électrons,
vaut dq.
Cas de la pile de fem e :
Etat initial des électrons sortant : E
pi
= E
-
. dq
Etat final des électrons rentrant : E
pf
= E
+
. dq
Variation d’énergie dW’ pour ces électrons du
système :
dW' = E
pf
– E
pi
= (E
+
- E
-
) . dq = e.dq < 0
( car dq < 0 )
Donc les électrons ont perdu de l’énergie, par
dissipation par effet Joule dans la résistance par
exemple, ou pour alimenter un moteur.
Cas de l’électrolyseur soumis à la fem e :
Etat initial des électrons sortant : E
pi
= E
+
. dq
Etat final des électrons rentrant : E
pf
= E
-
. dq
Variation d’énergie dW’ pour ces électrons du
système :
dW' = E
pf
– E
pi
= (E
-
- E
+
) . dq = -e.dq > 0
( car dq < 0 )
Donc les électrons ont gagné de l’énergie, énergie
fournie par le générateur.
Pour éviter d’avoir deux expressions différentes de dW’, énergie électrique échangée par les électrons, selon que le
système soit un récepteur ou un générateur, conventionnellement, on appellera dq la charge qui entre par la borne
de potentiel le plus élevé ( de sorte que dq pour un système pile ou générateur, est négative – cas intuitif - ) alors
que dans le cas d’un système électrolyseur, les électrons sortant de la borne + du système, on leur attribuera une
charge positive . Dans tous les cas, on notera e > 0 la fem aux bornes du système.
L’énergie échangée par dn électrons d’un système redox s’écrira toujours dW’ = e . dq
Cette énergie est < 0 pour un système redox générateur ( pile ), car dq < 0
Cette énergie est > 0 pour un système redox récepteur (électrolyseur), car dq conventionnellement > 0
Système
redox =
générateur
Système
redox =
électrolyseur
G
e
-
e
-
e
-
e
-

Thermo et cinétique des processus redox 3
2- B - V ARIATION ÉLÉMENTAIRE D ’ ENTHALPIE LIBRE DU SYSTÈME REDOX
Exprimons dU pour un système en réaction rédox:
dU = δQ + dW ← travail fourni par le système , soit dW = -PdV + dW' = -PdV + e . dq
donc dU= δQ -PdV + e . dq or H = U + PV => dH = dU + PdV + VdP
donc dH = δQ - PdV + e . dq + PdV + VdP
⇔ dH = δQ + e . dq + VdP or G = H - TS => dG = dH –TdS –SdT
⇔ dG = δQ + e . dq + VdP - T dS – SdT or dS = δS
e
+ δS
i
=
T
Q
δ
+ δS
i
⇔ dG = δQ + e . dq + VdP – T (
T
Q
δ
+ δS
i
) – SdT
⇔ dG = e . dq + VdP – TδS
i
– SdT
⇔ pour une transformation à T et P constants dG = e.dq – TδS
i
Cas général, pour une transformation irréversible :
Dans le cadre d’une transformation spontanée irréversible δS
i
> 0 => - TδS
i
<0 => dG
irr
< e.dq
Signification : Lorsque le système fonctionne comme un générateur (pile), le travail électrique reçu par l’extérieur
vaut –edq, positif. L’objectif est qu’il soit le plus positif possible. Or –e.dq < - dG ( valeurs positives ) : il est impossible
de récupérer toute l’énergie perdue par le système : une part de cette énergie est de la création d’entropie, perdue.
Lorsque le système travaille comme un récepteur ( électrolyse ) , l’énergie (positive) reçue par le système, dG, est
inférieure à l’énergie e.dq ( rappel dq est conventionnellement pris positif ) fournie par le générateur.
Cas particulier, pour une transformation réversible :
Dans le cadre d’une transformation réversible ou quasi statique, δS
i
= 0 => - TδS
i
=0 => dG
rev
= e.dq
Il s’agit de travailler dans des conditions proches de l’équilibre, c’est-à-dire en réalité, à courant circulant quasi nul, soit
une transformation de matière infiniment lente… ce qui n’est forcément pas adapté à l’usage souhaité pour les
systèmes redox.
On retiendra donc qu’une part de l’énergie électrochimique échangée est perdue sous forme entropique lors des
processus redox qui ne sont pas infiniment lents.
2- C - E NTHALPIE LIBRE DE RÉACTION REDOX
Soit une réaction redox se produisant dans les conditions de réversibilité électrochimique ( cad à une vitesse
infiniment lente ) . La réalisation suppose par exemple que la réaction est réalisée non pas en mélangeant l’oxydant et
le réducteur dans un même bécher, mais en les séparant dans 2 béchers, reliés par un pont salin, et par une
résistance quasi infinie, soit en contraignant la réaction à avoir lieu au sein d’une pile de fem e .
=> dG = e.dq
=> (dG/dξ)
T,P
= ∆
r
G(T) = e . (dq/dξ)
T,P
Soit une pile relative à deux couples : (-) Ox
1
, Red
1
// Ox
2
, Red
2
(+) e = E
+
- E
-
(n e-)
La réaction de fonctionnement de la pile est : ν
o2
Ox
2
+ ν
r1
Red
1
= ν
r2
Red
2
+ ν
o1
Ox
1
a
ox2
b
red1
0 0
a
ox2
- ν
o2
dξ b
red1
– ν
r1
dξ (ndξ) ν
r2
dξ ν
o1
dξ
La charge déplacée par la réaction pour un avancement dξ est: dq = -n
F
.dξ
où n la stœchiométrie des é
-
échangés dans la réaction globale.
donc dq/dξ = -n
F ⇔ ∆
r
G(T) = -n F e
pile

Thermo et cinétique des processus redox 4
On retrouve donc bien que ∆
r
G(T) < 0 , donc A > 0 => dξ > 0 puisque la réaction écrite est la réaction de
fonctionnement de la pile .
Soit une pile de polarité INCONNUE au moment de sa définition : ( ?) Ox
1
, Red
1
// Ox
2
, Red
2
( ?)
La réaction associée à la pile s’écrit dans l’ordre des réducteurs :
ν
o2
Ox
2
+ ν
r1
Red
1
= ν
r2
Red
2
+ ν
o1
Ox
1
La ddp notée E se définit par E = E
dte
– E
gche
= E
2
– E
1
ici
Donc E = e si la réaction de fonctionnement = la réaction associée
Et E = - e si la réaction de fonctionnement est l’opposée de la réaction associée.
Ainsi, pour une réaction redox quelconque :
∆
r
G(T) = - n
F
E où E = E
dte
– E
gche
Avec E
dte
= E (couple dont le réducteur est à dte)
Avec E
gche
= E (couple dont le réducteur est à gauche)
Conséquence : L’affinité A de la réaction et la ddp = E
dte
– E
gche
sont de même signe. Le calcul de la différence de
potentiel E
dte
– E
gche
permet de prévoir le sens spontané de la réaction écrite :
E
dte
– E
gche
> 0 <=> A > 0 <=> la réaction a spontanément lieu dans le sens direct
E
dte
– E
gche
< 0 <=> A < 0 <=> la réaction a spontanément lieu dans le sens indirect
Exercice 1
(1) 2BrO
3-
+ 5 Cl
2
+ 4 H
2
O = 10 ClO
-
+ Br
2
+ 10 H
+
(2) Cr
2
O
72-
+ 3 Hg + 14 H
+
= 2 Cr
3+
+ 3 Hg
2+
+ 7 H
2
O
(3) Cl
2
+ H
2
O = HClO + Cl
-
+ H
+
On supposera les gaz sous un bar, les espèces dissoutes à la même concentration de 0,1 mol.L
-1
a- pH = 1
b- pH = 10
Quel est le sens d’évolution des 3 systèmes précédents dans les 2 conditions de pH ci-dessus ?
BrO
3-
/ Br
2
ClO
-
/Cl
2
Cr
2
O
72-
/Cr
3+
Hg
2+
/Hg Cl
2
/Cl
-
HClO/Cl
2
E°(V) 1,5 0,40 1,33 0,85 1,36 1,63
Tous les éléments de résolution et résultats de l'exercice ci-dessous font partie des savoirs et savoir-faire exigibles.
Exercice 2 : a- Démontrer alors que
∆
r
G° (T) = -n
F
E° en précisant la définition du E° mentionné dans cette
formule, valide pour une réaction redox quelconque.
b- En déduire les expressions de ∆
r
H° et ∆
r
S° en fonction du coefficient de température de la pile défini
comme
dT
dE°
en V.K
-1
Exercice 3 : Application de l'exercice 2
Soit la pile Pt / H
2
( 1 bar ) / H
+aq
, Cl
-aq
/ AgCl
sol
/ Ag
Le coefficient de température de cette pile vaut –6.10
-4
V.K
-1
. En déduire l'enthalpie standard de réaction de la pile.
Donnée : E°(AgCl/Ag) = 0,222V à 25 °C.