vitesse force composante

Contrôle de physique n°5
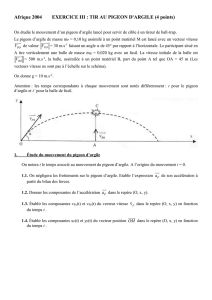
On étudie le mouvement d’un pigeon d’argile lancé pour servir de cible à un tireur de ball-trap.
Le pigeon d’argile de masse mP = 0,10 kg assimilé à un point matériel M est lancé avec un vecteur vitesse
uuur
PO
V
de valeur
uuur
PO
V
= 30 m.s-1 faisant un angle α de 45° par rapport à l’horizontale. Le participant situé
en A tire verticalement une balle de masse mB = 0,020 kg avec un fusil. La vitesse initiale de la balle est
uuur
BO
V
= 500 m.s-1, la balle, assimilée à un point matériel B, part du point A tel que OA = 45 m (Les
vecteurs vitesse ne sont pas à l’échelle sur le schéma).
On donne g = 10 m.s-2.
Attention : les temps correspondants à chaque mouvement sont notés différemment : t pour le pigeon
d’argile et t’ pour la balle de fusil.
1. Étude du mouvement du pigeon d’argile
On notera t le temps associé au mouvement du pigeon d’argile. A l’origine du mouvement t = 0.
1.1. On négligera les frottements sur le pigeon d’argile. Etablir l’expression
!
ap
de son accélération à
partir du bilan des forces.
Système : le pigeon.
Référentiel : terrestre supposé galiléen.
Repère : (O,x,y)
Bilan des forces : le "pigeon" n’est soumis qu’à son poids
!
P=mPg
(on néglige les forces de frottement).
On a donc :
!
"FExt =P=mPg
Application de la 2ème loi de Newton :
!
"FExt =mPaP#P=mPg=mPaP#
!
aP=g
1.2. Donner les composantes de l’accélération
!
ap
dans le repère (O, x, y).
On projette
!
ap
sur les axes Ox et Oy :
!
aP
aPx =0
aPy ="g
1.3. Établir les composantes vPx(t) et vPy(t) du vecteur vitesse
!
Vp
dans le repère (O, x, y) en fonction
du temps t .

Conditions initiales : les composantes de
!
VP0
sont :
!
VP0
VP0x=VP0.cos "
VP0y=VP0.sin "
A tout instant on a
!
aP=dVP(t)
dt
. En projetant sur les axes, on a alors :
• Selon Ox :
!
aPx =dVPx (t)
dt =0
. On cherche une primitive :
!
VPx (t)=cste
A t = 0 :
!
VPx (t=0) =VP0.cos " =cste #
!
VPx (t)=VP0.cos "
• Selon Oy :
!
aPy =dVPy (t)
dt ="g
. On cherche une primitive :
!
VPy (t)="gt +cste
A t = 0 :
!
VPy (t=0) =VP0.sin " =cste #
!
VPy (t)="gt +VP0.sin #
Les composantes de
!
VP(t)
sont donc :
!
v(t)VPx (t)=VP0.cos
"
VPy (t)=#gt +VP0.sin "
1.4. Établir les composantes xP(t) et yP(t) du vecteur position
!
OM
dans le repère (O, x, y) en fonction
du temps t .
Conditions initiales : les composantes de
!
OM
sont :
!
OM xP0=0
yP0=0
A tout instant on a
!
VP=dOM(t)
dt
. En projetant sur les axes, on a alors :
• Selon Ox :
!
VPx (t)=dxP(t)
dt =VP0.cos
"
. On cherche une primitive :
!
xP(t)=VP0.cos "
( )
.t+cste
A t = 0 :
!
xP(t=0) =0=cste "
!
xP(t)=VP0.cos " .t
• Selon Oy :
!
VPy (t)=dyP(t)
dt ="gt +VP0.sin
#
. On cherche une primitive :
!
yP(t)="1
2gt2+VP0.sin
#
( )
.t+cste
A t = 0 :
!
yP(t=0) =0=cste "
!
yP(t)="1
2gt2+VP0.sin
# .t
Les composantes de
!
OM(t)
sont donc :
!
OM(t)
xP(t)=VP0.cos " .t
yP(t)=#1
2gt2+VP0.sin
" .t
2. Tir réussi
2.1. Quelle est l’abscisse xC du point d’impact C du pigeon d’argile et de la balle ?
La trajectoire de la balle étant verticale, le point d’impact C se trouve à la verticale du point A. Donc
xC = xA. A.N. : xC = 45 m.

2.2. Vérifier, à partir de l’abscisse xC de l’impact, que le temps de « vol » du pigeon est Δt = 2,1 s.
Soit tC la date à laquelle le pigeon arrive au point C, le temps de vol Δt a donc pour valeur : Δt = tC - tO = tc.
On sait que
!
xP(t)=VP0.cos " .t
, d’où :
!
xC=VP0.cos " .tC#tC=xC
VP0.cos "
. D’où :
!
"t=xC
VP0.cos #
A.N. :
!
"t=45
30.cos 45°=2,1
⇒ Δt = 2,1 s.
Le temps de vol est bien de 2,1 s.
2.3. On néglige toutes les forces s’exerçant sur la balle.
2.3.1. Que peut-on dire de son accélération aB ? Que peut-on dire de sa vitesse vB ?
Déterminer alors la vitesse vB.
Système : la balle.
Référentiel : terrestre supposé galiléen.
Repère : (O,x,y)
Si on néglige toutes les forces s’exerçant sur la balle, on a
!
"FExt =0
: le mouvement est rectiligne
uniforme (accélération nulle et vitesse constante, 1ère loi de Newton), d’où : aB = 0 et VB = VB0.
A.N. : VB = 500 m.s-1.
2.3.2. Calculer Δt’ le temps de « vol » de la balle jusqu’à l’impact connaissant l’ordonnée
du point de l’impact yC = 22 m.
La vitesse étant constante, on peut utiliser la relation
!
VB="y
"t'# "t'="y VB
#
!
"t'=yC#yA
VB
A.N. :
!
"t'=22 #0
500 =0,044
⇒ Δt’ = 0,044 s.
2.4. Comparer Δt et Δt’ et expliquer pourquoi le tireur peut viser directement le pigeon.
!
"t
"t'=2,1 0,044 =48
⇒ Δt’ << Δt : le pigeon ne se déplace quasiment pas pendant le trajet de la balle. On peut
donc viser directement dans la direction du pigeon.
3. Discussion de l’effet du poids de la balle
Dans cette partie l’effet du poids de la balle n’est plus négligé mais on négligera toujours la force
de frottement de l’air.
3.1. Établir que la composante de la vitesse vBy(t’) dans le repère (O,x,y) vérifie l’équation
vBy(t’) = vB0 – g t’.
Bilan des forces : la balle n’est soumise qu’à son poids
!
P=mBg
(on néglige les forces de frottement).
On a donc :
!
"FExt =P=mBg

Application de la 2ème loi de Newton :
!
"FExt =mBaB#
!
aB=g
.
On projette
!
aB
sur l’axe Oy :
!
aBy ="g
. On sait que
!
aBy =dVBy (t')
dt'="g
, on cherche donc une primitive
pour VBy(t’) :
!
VBy (t') ="gt'+cste
.
Condition initiale : à t’ = 0 on a VBy(t’=0) = VB0 = cste d’où :
!
VBy (t') =VB0"gt'
.
3.2. Calculer la vitesse vBy au bout d’un temps Δt’ = 0,044 s, justifier pourquoi on a négligé le
poids dans la partie 2.
Δt’ = t’ - tA = t’, or :
!
VBy (t') =VB0"gt'#
!
VBy (t') =VB0"g.#t'
A.N. :
!
VBy (t') =500 "10 #0,044 =499,56 $500
. VBy(Δt’) ≈ 500 m.s-1, on peut donc bien considérer la
vitesse comme constante sur le trajet AC, le mouvement est alors rectiligne et uniforme. D’après la 1ère loi
de Newton, on aurait donc :
!
"FExt =0
. On peut négliger le poids de la balle sur ce trajet.