Méthode de Newton

Méthode de Newton
Fiche élève
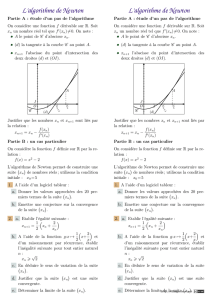
Comment calculer la valeur de p2 ?
Ne «bottons pas en touche »en répondant qu’il suffit de prendre une calculatrice
car la question devient alors : comment la calculatrice fait-elle pour calculer p2, ou
de façon plus précise, quel algorithme a été programmé dans la machine ?
Cette activité a pour but d’étudier un algorithme particulièrement efficace qui uti-
lise le calcul différentiel. Cet algorithme a été proposé par Isaac Newton, l’un des
inventeurs du calcul différentiel.
De quel nombre voulons nous parler lorsque nous écrivons p2 ? Il est nécessaire de le
savoir pour espérer en calculer une valeur. La réponse est qu’il s’agit de l’unique nombre
positif dont le carré vaut 2.
Si nous désignons par fla fonction définie sur [0 ; +∞[par f(x) = x2−2 alors p2 est
le nombre xtel que f(x) = 0.
La méthode de Newton résoud cette équation de manière itérative. Cela signifie qu’elle
procède par étapes successives et que chaque nouvelle étape permet d’obtenir une va-
leur approchée de p2 plus précise que celle obtenue à l’étape précédente. On arrête le
processus lorsqu’on estime que la valeur obtenue est suffisamment précise.
Le texte ci-dessous décrit l’algorithme utilisé par Newton en 1669 et par votre calculatrice
aujourd’hui :
Données :
Une fonction f
Un nombre uinitial
Un nombre efixant la condition d’arrêt du calcul
Résultat :
Un nombre utel que f(u)¶e
Traitement :
Tant que |f(u)|>e
Calculer l’accroissement ponctuel de fen u
Déterminer l’équation de la tangente au point d’abscisse u
Calculer l’abscisse du point d’intersection de la tangente avec l’axe des abscisses
Appeler ucette abscisse
Afficher la valeur de u
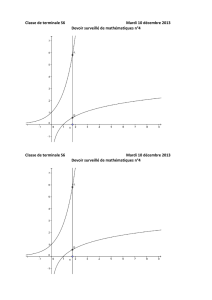
1. Voici une version graphique de l’algorithme :
Données :
La courbe d’une fonction f
Un nombre uinitial
Un nombre efixant la condition d’arrêt du calcul
Résultat :
Un nombre utel que f(u)¶e
Traitement :
Tant que |f(u)|>e
Calculer le coefficient directeur de la courbe de fau point d’abscisse u
Tracer la tangente au point d’abscisse u
Marquer le point d’intersection de la tangente avec l’axe des abscisses
Appeler ucette abscisse
Lire la valeur de u
Exécutez cette version sur l’annexe ci-jointe en choisissant 15 comme valeur ini-
tiale de uet 3 comme valeur pour e. Dessinez les tangentes et marquez les points
d’intersection avec l’axe des abscisses.
2. Exécutez la version initiale de l’algorithme avec les mêmes données : u=15 et e=3.
Détaillez pour chaque itération les calculs qui fournissent l’équation de la tangente
puis ceux qui fournissent l’abscisse de son point d’intersection avec l’axe des abs-
cisses.
3. Traduisez l’algorithme de Newton en un programme dans le langage de votre calcu-
latrice ou si vous préférez dans le langage Python.
Dans les deux langages |a|s’écrit «abs(a) ».
4. (a) Programmez l’algorithme dans votre calculatrice et utilisez le pour calculer
une valeur approchée de p2 en prenant comme données initiales u=15 et
e=0,000 001.
Donnez la valeur approchée de p2 que vous obtenez.
(b) Combien d’itérations a exécuté votre programme ?
Modifiez légèrement votre programme pour le savoir.
http://dichotomies.fr/2011/infomath/activites/fonctions/methode-de-newton/fiche-eleve/ Denis Pinsard – Mis à jour le lundi 21 novembre 2011 [CML033]

ANNEXE A – Méthode de Newton
0
10 20 30 40 50 60 70 80 90
100 110 120 130 140 150 160 170 180 190 200 210 220
−10
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
x
f(x)
http://dichotomies.fr/2011/infomath/activites/fonctions/methode-de-newton/fiche-eleve/ Denis Pinsard – Mis à jour le lundi 21 novembre 2011 [CML033] Page 2