Devoir n°4 - j.galtier

Classe de terminale S6 Mardi 10 décembre 2013
Devoir surveillé de mathématiques n°4
Classe de terminale S6 Mardi 10 décembre 2013
Devoir surveillé de mathématiques n°4

Exercice 1 (d’après bac S, Antilles 2011, 15 points)
Dans une large mesure, les quatre parties sont indépendantes
On appelle la fonction définie sur R par
.
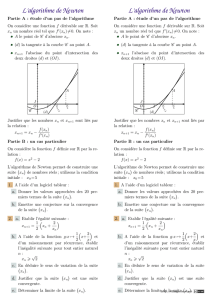
Partie A :
1. On admet que
. Quelle est la conséquence pour la courbe de ?
2. Calculer , étudier les variations de .
3. Montrer que l’équation admet une solution unique . Donner un
encadrement de entre deux entiers consécutifs.
4. Soit une primitive de . Sans chercher à calculer , donner son tableau de
variations.
Partie B :
On considère maintenant la suite
définie par
et pour tout ,
.
1. Montrer par récurrence que, pour tout ,
.
2. En déduire que la suite
est croissante.
3. Montrer que la suite
converge. On appelle sa limite.
4. Montrer que . En déduire la valeur de .
5. Donner à la calculatrice la plus petite valeur de telle que
!
.
Partie C :
On désire obtenir un encadrement d’amplitude 10
-6
de . On a écrit un algorithme de
balayage, et un algorithme de dichotomie
Balayage :
Variable :
prend la valeur 0
Tant que "#
"
" prend la valeur " $
Fin tant que
Afficher
Dichotomie
Variables % &%
prend la valeur 0
& prend la valeur 1
Tant que & '
(
prend la valeur
)
*
Si "#
"
+ alors , prend la valeur
Sinon
Fin si
Fin tan que
Afficher
1. Compléter les lignes en gras (attention, on veut un encadrement de )
2. Sachant que la solution vaut environ - %./, combien l’algorithme de balayage a-t-
il répété sa boucle ?
3. Dans l’algorithme de dichotomie, comment évolue la longueur 0 à chaque
itération ? Combien faut-il d’itérations pour obtenir un encadrement d’amplitude
(
de ?
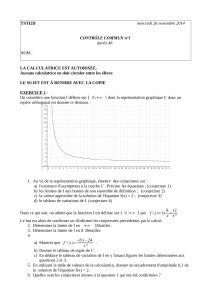
Partie D :
On a tracé ci-dessous les courbes des fonctions
et 1. est un réel positif 2
et 3 sont les points de ces courbes d’abscisse . On rappelle que, pour tout ,
' 1.
1. Exprimer la distance 23 en fonction de .
2. Montrer que 23 est minimale quand est égal à
3. Démontrer que
4
4
, en déduire que la distance 23 minimale est $
4
.
4. Montrer qu’au point d’abscisse , les tangentes aux deux courbes sont parallèles.

NOM :
Exercice 2 (5 points)
À traiter séparément sans calculatrice. Les questions sont indépendantes.
1. Calculer la dérivée des fonctions suivantes :
a)
!56
7
b) 89: $ .; :
*
2. Donner une équation de la tangente à la courbe de (de la question 1) en son point
d’abscisse 1
3. Donner une primitive des fonctions suivantes :
a) < ; 1 = $
>
b) ?: $ :
7*!
4. Soit la fonction définie par $ 0
!
où % 0 sont deux constantes.
a) Calculer
@
en fonction de et 0.
b) Déterminer les valeurs de et 0 telles que soit une primitive de la fonction
définie par
!

NOM :
Exercice 2 (5 points)
À traiter séparément sans calculatrice. Les questions sont indépendantes.
1. Calculer la dérivée des fonctions suivantes :
a)
*56
7
b) 89A $ ;: A
*
2. Donner une équation de la tangente à la courbe de (de la question 1) en son point
d’abscisse 1
3. Donner une primitive des fonctions suivantes :
a) < .
/ $
>
b) ?
*
7*
4. Soit la fonction définie par $ 0
*
où % 0 sont deux constantes.
a) Calculer
@
en fonction de et 0.
b) Déterminer les valeurs de et 0 telles que soit une primitive de la fonction
définie par
*
1
/
4
100%