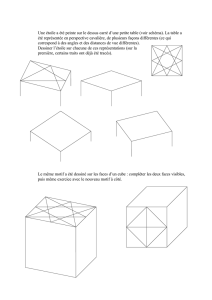
Solides PE2

Solides
(D’après « Donner du sens aux mathématiques, Tome 1 Espace et Géométrie » Bordas)
Quelques définitions
En géométrie, on appelle solide toute figure indéformable à 3 dimensions, limitée par une surface fermée.
Il existe deux types de solides : les polyèdres délimités par une surface uniquement composée de
polygones, et les non polyèdres. Un non polyèdre est un solide dont l’une, au moins, des parties de la
surface le constituant n’est pas un polygone.
Exemples : Le cube est un polyèdre. Il est délimité par des carrés. Le cône de révolution n’est pas un
polyèdre. Il n’est pas délimité par des polygones. De même, la surface d’un cylindre de révolution
comportant des disques, le cylindre n’est pas un polyèdre.
Les polyèdres
Les polygones délimitant le polyèdre sont appelés les faces du polyèdre. Les côtés communs des
polygones qui constituent les faces sont appelés les arêtes du polyèdre et les sommets des polygones
restent appelés sommets pour le polyèdre.
Exemple : Un pavé droit a 6 faces, 8 sommets et 12 arêtes.
Remarque : Le mot face n’est utilisé que pour les polyèdres.
Déterminer le nombre de faces d’un cylindre n’a aucune signification puisque le cylindre n’est pas un
polyèdre.
Un polyèdre est dit convexe s’il se situe d’un même côté de tous les plans support des faces. On peut
encore dire qu’un polyèdre convexe est tel que quelle que soit la façon dont on le pose sur une surface
plane, il repose sur une face entière. S’il n’est pas convexe, il est dit concave. On reconnaît qu’un
polyèdre est concave si deux de ses faces forment « un creux ».
Pour vérifier le nombre de faces, d’arêtes, de sommets d’un polyèdre convexe, on peut utiliser la relation
d’Euler : si a est le nombre d’arêtes, s le nombre de sommets, f le nombre de faces alors s + f = a + 2

Polyèdres particuliers
1.Polyèdre régulier
Un polyèdre est régulier lorsque :
- il est convexe
- toutes ses faces sont des polygones réguliers identiques
- de chacun de ses sommets partent le même nombre d’arêtes formant le même angle.
Par exemple, un cube est un polyèdre régulier, un octaèdre dont les huit faces sont des triangles
équilatéraux identiques est un polyèdre régulier mais un hexaèdre dont les six faces sont des triangles
équilatéraux identiques n’est pas un polyèdre régulier puisque la troisième condition n’est pas vérifiée.
Il existe seulement cinq polyèdres réguliers :
- le cube
- le tétraèdre régulier dont les quatre faces sont des triangles équilatéraux identiques
- l’octaèdre régulier dont les huit faces sont des triangles équilatéraux identiques
- l’icosaèdre régulier dont les vingt faces sont des triangles équilatéraux identiques
- le dodécaèdre régulier dont les douze faces sont des pentagones réguliers identiques.
2.Prisme
Un prisme droit est un polyèdre dont la surface est composée de deux polygones identiques et parallèles
appelés bases, et de rectangles qui constituent les faces latérales.
Exemples : - Un cube est un prisme droit dont les bases et les faces latérales sont des carrés.(Le carré
est un rectangle particulier.)
- Un parallélépipède rectangle ou pavé droit est un prisme droit dont les bases et les faces latérales sont
des rectangles. (Les faces latérales peuvent aussi être des carrés. Le cube est un parallélépipède
rectangle particulier)
Un prisme non droit est composé de deux bases, qui sont des polygones identiques et parallèles, et dont
certaines faces latérales sont des parallélogrammes non rectangles.
3.Pyramide
Une pyramide est un polyèdre dont la surface est composée d’un polygone appelé base et de triangles
ayant un sommet commun.
Exemple : Un tétraèdre est une pyramide dont la base est un triangle. Il est donc composé de quatre
triangles. Un tétraèdre régulier est une pyramide composée de quatre triangles
équilatéraux identiques.
Solides particuliers non polyèdres
1.Cylindre de révolution
Un cylindre de révolution est un solide engendré par la rotation d’un rectangle autour de l’un de ses côtés.
Il est donc formé par deux disques, identiques et parallèles, et par une surface non plane. Les deux
disques s’appellent les bases du cylindre.
2.Cône de révolution
Un cône de révolution est un solide engendré par la rotation d’un triangle rectangle autour d’un des côtés
de l’angle droit. Il est donc formé par un disque et une surface non plane.
On omet souvent de préciser le qualificatif « de révolution » lorsqu’on évoque le cylindre et le cône.
Pourtant, il existe d’autres types de cylindre et de cônes avec des bases qui ne sont pas des disques,
mais par exemple des ellipses.
3.Boule
Une boule est un solide délimité par une surface appelé sphère. Une sphère de centre O et de rayon R
est une surface constituée par l’ensemble des points dont la distance à O est égale à R.

Représentations planes des solides
Plusieurs représentations d’un solide sur un plan peuvent être envisagées : une perspective centrale, une
perspective parallèle (cavalière ou axonométrique), une représentation des différentes vues, un patron.
Ce passage de l’espace à la représentation plane entraîne la perte de certaines informations. C’est ce qui
explique l’existence de plusieurs types de représentations planes, chacune conservant et transmettant
certaines informations au détriment d’autres. 1
Une représentation ne peut rendre compte à la fois de la vision d’un objet et de ce que l’on sait de lui. On
retrouve le conflit entre le « voir » et le « savoir ». Il faut alors prendre en compte ce qu’on attend d’une
représentation.
Perspective cavalière
La perspective cavalière résulte d’une projection oblique sur un plan appelé plan de projection. La
projection se fait dans une même direction.
Exemple 1 : Cube projeté sur un plan parallèle à la face de devant.
Pour comprendre la projection permettant de donner cette représentation à partir d’un cube posé sur un
plan horizontal, on peut imaginer des segments obliques et parallèles partant de chaque sommet du cube
et arrivant sur un plan vertical. La figure, formée sur ce plan, en reliant les points intersections des
segments et du plan vertical, est une perspective cavalière du cube.
Cette figure ne contient véritablement que deux carrés. Pourtant, elle représente un cube constitué de six
carrés. Les faces parallèles au plan de projection ne sont pas déformées. De façon générale, les éléments
situés dans des plans parallèles au plan de projection sont conservés. Les arêtes du cube qui sont
perpendiculaires au plan de projection sont représentées par des droites parallèles appelées fuyantes.
L’angle formé par ces fuyantes et la direction horizontale caractérise la perspective cavalière choisie, le
plus souvent l’angle est égal à 45°, mais parfois i l peut aussi valoir 30°. Les dimensions des segment s
portés par les fuyantes sont, en général, réduites par rapport aux dimensions réelles. Le rapport de
réduction est aussi une caractéristique de la perspective cavalière.
Le parallélisme des droites est conservé ainsi que le rapport des longueurs de segments parallèles.
Pour des éléments qui ne sont pas situés dans des plans parallèles au plan de projection, les distances,
les angles ne sont pas conservés ce qui peut être traduit par la non conservation des formes géométrique
des faces.
L’alignement des points est conservé : des points alignés dans l’espace le sont sur la représentation mais
la réciproque est fausse en général. Des droites qui paraissent se couper sur la représentation peuvent ne
pas être concourantes dans la réalité.
1 D’après l’ouvrage Rouche N., Lismont L. (2001) , Formes et mouvements. Perspectives pour l’enseignement de la
géométrie, Centre de recherche de l’enseignement des mathématiques

Perspective centrale
Exemple du cube :
Les angles, le parallélisme, l’orthogonalité, les longueurs, les rapports de longueur ne sont en général pas
conservés dans ce type de représentation. Par contre, la forme et les rapports de longueur d’un objet
situé dans un plan parallèle au plan de projection sont conservés.
Remarque : on peut envisager aussi des perspectives centrales avec plusieurs points de fuite mais à
l’école élémentaire seule la perspective centrale à un point de fuite est abordée par l’utilisation de photos.
Ces dernières ont l’avantage de fixer le plus fidèlement possible la perception visuelle et ainsi d’en
permettre la conservation.
Projections orthogonales (Vues)
Une vue d’un solide est une représentation plane qui provient d’une projection orthogonale sur un plan
parallèle à une face.
Exemple : Vue de dessus d’un cube.
Pour comprendre la projection permettant d’obtenir cette vue de dessus à partir d’un cube posé sur un
plan horizontal, on peut imaginer des segments verticaux partant des sommets du solide et arrivant sur un
plan horizontal.
Suivant le plan sur lequel le solide est projeté, différentes vues sont possibles : vue de dessus (le plan est
parallèle à la face de dessus), vue de droite (le plan est parallèle à la face de droite), vue de face…
Le dessin technique utilise ce type de représentation. Pour qu’un objet puisse être construit à partir des
différentes vues, trois vues sont nécessaires : vue de face, de droite, de dessus ainsi que des conventions
de traçage. En particulier, ce qui est vu est formé avec des traits pleins, ce qui est caché avec des traits
en pointillé
On peut aussi évoquer le mot « empreinte ».
Pour un prisme droit posé sur sa base, la vue de dessus correspond à l’empreinte du prisme. La vue de
dessus du cube donné en exemple précédemment correspond à l’empreinte du cube. Par contre, pour un
solide quelconque, l’empreinte est souvent différente de la vue de dessus. L’empreinte d’une boule est un
point alors que sa vue de dessus est un disque. On pourrait dire que la vue de dessus est le « trou » que
ferait un solide dans un plan si on l’enfonçait perpendiculairement à ce plan. On a ainsi une bonne
illustration d’un exemple d’une projection orthogonale d’un solide pour des élèves de l’école élémentaire
Patron
Un patron d’un solide est une surface plane qui permet de reconstruire le solide uniquement par pliage et
sans recouvrement ; ou, en reprenant la définition de S.Gobert (2001), « un patron de solide est un
dessin, où toutes les faces du solide sont représentées, toutes juxtaposées les unes aux autres,
permettant après découpage du contour et pliage suivant les segments, de reconstituer le solide en
volume » 2 . Le terme de développement du solide s’emploie quelquefois à la place du mot patron.
S.Gobert (ibid.) effectue deux types de remarques : celles concernant le patron à partir du solide et celles
concernant le solide à partir du patron.

A partir du patron :
« Deux faces adjacentes sur le patron sont toujours adjacentes sur le solide. Mais attention, deux faces
qui ne sont pas l’une à côté de l’autre sur le patron peuvent être des faces adjacentes sur le solide, ou ne
pas être des faces adjacentes sur le solide. »
« Un segment commun à deux faces sur le patron est une arête du solide. Mais on peut avoir deux
segments sur le patron qui correspondent à une même arête du solide »
A partir du solide :
« Deux faces adjacentes sur le solide peuvent être adjacentes sur le patron ou ne pas l’être. Par contre,
deux faces non adjacentes sur le solide ne peuvent jamais être adjacentes sur le patron »
« Une arête d’un solide peut être représentée une ou deux fois sur un patron du solide »
« Un sommet du solide peut être représenté par un ou plusieurs points sur le patron » 3
« Ces connaissances sont en jeu dans les activités proposées en général aux élèves. Elles sont très
rarement formulées, et pourtant elles permettent d’avoir des repères qui peuvent faciliter, améliorer, faire
progresser la capacité à remonter un patron en volume dans sa tête et à lire sur les patrons les propriétés
du solide » 4
Un polyèdre peut avoir plusieurs patrons différents. Exemple : Le cube a onze patrons.
Certains solides ne sont pas développables ; ils n’ont pas de patron. Exemple : La boule.
2 GOBERT S.(2001) Questions de didactique liées au rapport entre la géométrie et l’espace sensible, dans le cadre de
l’enseignement à l’école primaire, thèse Université Paris VII: p. 143
3 GOBERT S.(2001) : p. 143
4 GOBERT S.(2001) : p. 143