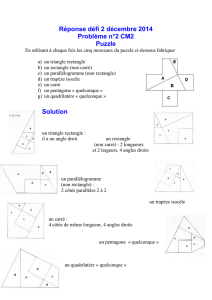
rectangle d`or et spirale

Devoir Maison de Mathématiques
Vous allez créer une suite de nombres. Les 2 premiers sont 0 et 1. Chaque nombre suivant est la somme des
2 nombres précédents. On l’appelle suite de Fibonacci.
1) Donner la liste des 30 premiers nombres de la suite.
2) Calculer les quotients obtenus en divisant un nombre de la suite par son prédécesseur.
Que constatez-vous? Vous venez de découvrir une valeur approchée du nombre d’or.
3) Réaliser le programme de construction suivant:
- Construire un carré ABCD de côté 1 dm. On appelle I le milieu du segment [AB]
- Tracer le cercle de centre I, de rayon [IC]. Ce cercle coupe la demi-droite [AB) en E.
- Construire le rectangle AEFD.
Remarque : le rectangle AEFD est appelé rectangle d'or car la proportion entre sa longueur et sa largeur est
égale au nombre d'or. Vérifier cela dans votre construction.
4) Réaliser cette spirale d’or en prenant comme rectangle de départ le
rectangle d’or précédent.
( le rectangle d’or est découpé en un carré et un autre rectangle, on répète
alors l’opération avec le nouveau rectangle)
Vous vérifierez que chaque rectangle est bien un rectangle d’or.
5) Le nombre d'or est le nombre irrationnel noté par la lettre grecque φ (prononcé phi) et égal à
. Montrer que le nombre d’or est solution de l’équation :
1+ √ 5
2
x ²−x−1=0
6) Trouver des exemples de rectangles d’or dans la peinture.
Devoir Maison de Mathématiques
Vous allez créer une suite de nombres. Les 2 premiers sont 0 et 1. Chaque nombre suivant est la somme des
2 nombres précédents. On l’appelle suite de Fibonacci.
1) Donner la liste des 30 premiers nombres de la suite.
2) Calculer les quotients obtenus en divisant un nombre de la suite par son prédécesseur.
Que constatez-vous? Vous venez de découvrir une valeur approchée du nombre d’or.
3) Réaliser le programme de construction suivant:
- Construire un carré ABCD de côté 1 dm. On appelle I le milieu du segment [AB]
- Tracer le cercle de centre I, de rayon [IC]. Ce cercle coupe la demi-droite [AB) en E.
- Construire le rectangle AEFD.
Remarque : le rectangle AEFD est appelé rectangle d'or car la proportion entre sa longueur et sa largeur est
égale au nombre d'or. Vérifier cela dans votre construction.
4) Réaliser cette spirale d’or en prenant comme rectangle de départ le
rectangle d’or précédent.
( le rectangle d’or est découpé en un carré et un autre rectangle, on répète
alors l’opération avec le nouveau rectangle)
Vous vérifierez que chaque rectangle est bien un rectangle d’or.
5) Le nombre d'or est le nombre irrationnel noté par la lettre grecque φ (prononcé phi) et égal à
. Montrer que le nombre d’or est solution de l’équation :
x ²−x−1=0
6) Trouver des exemples de rectangles d’or dans la peinture.
1+ √ 5
2