Sujet 2008 - Société Tunisienne de Physique

Exercice N°1
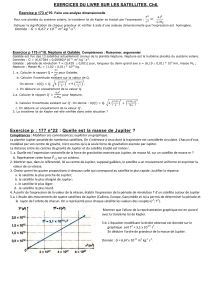
Un système (S) en rotation est constitué d’une poulie homogène de rayon R = 6 cm, d’une
tige, et de deux solides A et B supposés ponctuels de même masse m fixés aux extrémités de
la tige. Le système (S) est mobile autour d’un axe fixe
)
(
∆
horizontal passant par le centre O
de la poulie (voir figure ci-dessous). Le moment d’inertie de (S) par rapport à
)
(
∆
est :
J = 7,2. 10
4
−
kg. m
2
Un fil inextensible de masse supposée
nulle est attaché par l’une de ses
extrémités à un solide (S
1
) de masse
m
1
= 200 g et par sa deuxième extrémité
à un solide (S
2
) de masse m
2
= 4 m
1
. Le
fil passe sans glisser sur la gorge de la
poulie.
(S
1
) est placé sur un plan rugueux incliné d’un angle
α
= 45° par rapport à l’horizontale. Le
plan exerce sur (S
1
) des frottements constants de valeur
f = 0,5
r
N.
(S
2
) est placé sur un plan parfaitement lisse et incliné d’un angle
β
= 30° par rapport à
l’horizontale. On désigne par
g
r
le vecteur champ de pesanteur du lieu considéré.
Lorsque le système est abandonné sans vitesse initiale à un instant de date t = 0, le solide
(S
2
) prend un mouvement rectiligne descendant.
1) a- Ecrire la relation fondamentale de la dynamique pour chacun des solides (S
1
), (S
2
) et
pour le système (S).
b- Montrer que la valeur de l’accélération a des solides (S
1
) et (S
2
) est de la forme:
REPUBLIQUE TUNISIENNE
MINISTERE DE L’EDUCATION ET DE LA FORMATION
CONCOURS NATIONAL DE PHYSIQUE
PROPOSE PAR LA SOCIETE TUNISIENNE DE PHYSIQUE
SESSION : AVRIL 2008 DUREE : 2
H
Toute calculatrice non programmable est autorisée.
Au cours de la correction, la présentation de la copie est prise en considération.
(S
1
)
(S
2
)
B
A
α
β
O
(
∆
)
(S)

a
1
12
m g (4sin
β - sinα) - f
J
5m +
R
=
r r
. En déduire sa valeur numérique.
2) Calculer la vitesse angulaire du système en rotation à l’instant de date t
1
= 10 s.
3) A cet instant t
1
, le fil est coupé et, sous l’effet d’un couple de freinage exercé sur la poulie,
le système en rotation s’arrête après avoir effectué 10 tours.
Déterminer la valeur du moment M
C
du couple de freinage supposé constant et la durée,
comptée à partir de la date t
1
, mise par le système pour s’arrêter. On prendra:
-2
g = 10 m.s
r
Exercice N°2
On se propose de déterminer la masse M de Jupiter en étudiant le mouvement de ses
principaux satellites: Io, Europe, Ganymède et Callisto.
1/ Le mouvement d’un satellite, de masse m, est étudié dans un repère considéré comme
galiléen, ayant son origine au centre de Jupiter et ses axes dirigés vers des étoiles lointaines
considérées comme fixes.
a- En supposant que Jupiter et ses satellites ont une répartition de masse à symétrie sphérique
et qu’un satellite (S
1
) se déplace sur une trajectoire circulaire, à la distance R
1
du centre de
Jupiter, déterminer la nature du mouvement de (S
1
) et l’expression qui relie la valeur
v
r
de
sa vitesse à R
1
, à la masse M et à la constante de gravitation universelle G.
b- En déduire 1’expression de la période T
1
de révolution du satellite.
c- Montrer que, pour un satellite mobile sur une trajectoire circulaire de rayon R avec une
période T, le rapport 3
2
R
T
est constant.
2/ Par des méthodes de mesures appropriées, les périodes de révolution et les rayons des
orbites des satellites de Jupiter ont été déterminés. Leurs valeurs sont consignées dans le
tableau suivant :
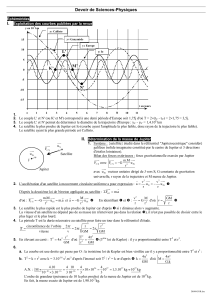
En utilisant les données du
tableau, on représente dans un
système d’axes, le graphe
donnant les variations de T2 en fonction de R3 (voir graphe ci-dessous).
a-A partir du graphe,
écrire l’équation qui relie
T2 à R3.
b- Déduire la masse M
de Jupiter.
On donne:
La constante G de
gravitation universelle :
G = 6,67.10
-11
N .m
2
kg
-2
.
Satellite Io
Europe Ganymède Callisto
Période T (heure) 42,5 85,2 171,7 400,5
Rayon R (10
6
m) 422 671 1070 1883
T
2
R
3
0
4.10
26
m
3
4.10
11
s
2

Corrigé
Exercice N°1
1°/ La relation fondamentale de
la dynamique pour :
Le système : {(S1)}
Repère galiléen.
Bilan des forces :
(S1) est soumis à son poids
1
P
r
à la réaction
1
R
r
du plan et
à la tension:
1
T
r
du fil
Par application du théorème du
centre d’inertie on peut écrire :
1 1 1 1 1
P + R +T = m .a
r r r
r
Projection suivant (x’x) :
1 1 1 1
- P sin
α - f + T = m .a
r
r r
Le système : {(S2)}
Repère galiléen.
Bilan des forces :
2 2 2
P , R , T
r r r
Par application du théorème du centre d’inertie on peut écrire :
2 2 2 2 2
P + R + T = m .a
r r r
r
Projection suivant (
'
y y
)
2 2 2 2
p sin
α - T = m a
r
r
Le système {(S)}
Bilan des forces : (S) est soumis à son poids
P
r
, à la réaction
R
r
3 de l’axe de rotation (
∆
), à la
tension
1
T'
r
du fil soutenant (S1) et à la tension
2
T '
r
du fil soutenant (S2).
Par application de la relation fondamentale de la dynamique à la poulie, on peut écrire :
''.
/'/'/
/
21
θ JMMMM
TTPR
=+++
∆∆∆
∆rrrr
0
0
/
/
=
=
∆
∆
R
P
M
M
r
r
car
R
r
3 et
P
r
rencontrent l’axe (∆)
2 1
T ' .R - T ' .R = J.
θ''
ur ur
b) La valeur de l’accélération a :
Comme le fil et inextensible et passe dans la même gorge de la poulie donc :
1 2
a = a = a
' '
1 1 2 2
T = T et T = T
r r r r
(S
1
)
(S
2
)
B
A
α
O,
x’
x y’
y
β

1 1 1
12
2 2 2
2 1 1 2
1 1 1
1 1
- f + T - P .sinα = m .a
a
- T .R + T .R = J.R
P sinβ - T = m .a
J
R. P sin
β - P R.sinα - f R = a(m R + m R + )
R
J
- f R - m g Rsin
α + 4m g Rsinβ = a(5m R + )
R
R[m g (4sinβ - sinα) - f ] = a(5m
r
r
ur uur
uur r
uur ur r
r r r
r r
2
1-2
12
J
+ )R
R
m g (4sinβ - sinα) - f
a = a = 1,74 m.s
J
5m +
R
⇒
r r
2) La vitesse angulaire du système en rotation à l’instant de date t
1
= 10 s.
-1
1
atv
θ' = θ' = θ' = 290 rad.s
R R
⇒ ⇒
3) La valeur du moment MC du couple de freinage
Système
{
}
tige, Poulie
Bilan des forces :
P, R et le couple des forces de frotteme
nt
ur uur
.
1
///
''.
θ
JMMM
fRP
=
+
+
∆∆∆
1
/
''.
θ
JM
f
=
∆
MC
Comme le moment du couple MC de frottement est constant
θ
’’ est alors constante et le
mouvement du système est uniformément varié, on peut donc écrire :
2 2
2 1 1 2 1
2 2
-2
1
12 1
f/∆1
θ' - θ' = 2θ''(θ - θ)
θ' 290
θ'' = - = - = - 669 rad.s
2(θ-θ) 40π
M = J.θ'' = - 0,48 N.m
La valeur de la durée mise par le système pour s’arrêter :
On a : = -669t+290 ; = 0 si t = 290/669 = 0,43 s
Le système s’arrête après une durée de 0,43 s

Exercice N°2
1/
a-
{
}
Système = Satellite
La force qui agit sur le satellite (S
1
) et dirigée vers Jupiter
est
1
J/S
F
r
telle que :
1
J/S 2
1
G.m.M
F = R
uuur
Par application de la loi fondamentale de la
dynamique on peut écrire :
F = m.a
r r
.
Dans le repère de Frénet, on peut écrire :
T
2
n2
1 1
dv
m.a = m = 0
dt
m.a
m.v G.m.M
m.a = =
R R
r
ste
dv = 0 v = C
dt
⇒ ⇒
le mouvement du satellite est circulaire uniforme. Il se fait avec une
vitesse angulaire
ω
constante
2
1
G.M
v =
R
2 2 2
1
3
1
G.M
= R ω ω =
R
⇒
b-
2 3 3
2
21 1
1 1
2
4
π R R
4 π
T = = T = 4 π
ω G.M G.M
⇒
c-
2 2
3
T 4
π
=
R G.M
= C
te
2 / Le graphe représentant T
2
= f (R
3
) est une droite linéaire de pente "a" égale à :
a =
M
G
.
4
2
π
≈
0,31
×
10
15 −
La masse M de Jupiter est égale à M =
2
4
π
G . a
≈
2
-11 -15
×
4×π
6,67 10 ×0,31×10
≈
1,9
27
10 kg
×
2
2
1 1
m.v G.m.M
=
R R
SJ
F
/
r
τ
r
n
r