Classe de Première S Champs et forces Devoir à la maison

Classe de Première S  Champs et forces  Devoir à la maison 
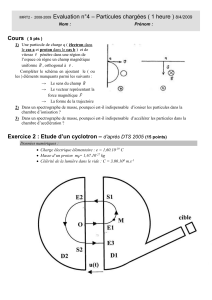
Le fonctionnement du cyclotron
Le cyclotron a été inventé au début des années 30
par Ernest Lawrence et Milton Livingston. C'est un
des premiers accélérateurs de particules à
combiner les champs magnétiques et
électrostatiques pour donner une trajectoire en
forme de "spirale" à des protons et les monter à
une énergie allant de quelques MeV.
Un record pour l'époque !
Lawrence et Milton posent en 1932 à côté d'un cyclotron.
Un de leur cyclotron avait un rayon de 14cm.
Ce modèle fonctionnait sous une tension maximale
de 4000V et une fréquence de 17,2MHz. Les
protons avaient en sortie une énergie de 1,2MeV.
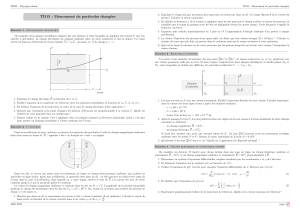
Principe du cyclotron :
Dans une chambre d'accélération où règne un vide
très poussé, deux cavités en forme de demi-
cylindre (appelées Dees) se font face par la
tranche, séparées par un petit intervalle, appelé
zone de coupure d'épaisseur d.
Un champ magnétique
⃗
B
, uniforme, est créé
dans toute la chambre par un puissant électro-
aimant. Ce champ magnétique, vertical, dirigé vers
le haut, est aligné sur l'axe des demi-cylindres.
Un champ électrostatique
⃗
E
est établi dans la
zone de coupure grâce à une tension U de la
même façon que dans un condensateur plan.
Ce champ est donc perpendiculaire aux tranches des demi-cylindres. Le sens du champ électrique doit
être inversé régulièrement et synchronisé sur le sens de traversée de la zone de coupure par le proton.
Pour cette raison, la tension U est une tension périodique et alternative. Ce champ permet d'augmenter
la vitesse des protons à chaque fois qu'ils traversent la zone de coupure. On admettra que les protons
traversent la zone de coupure en un temps négligeable et quand la tension U est à son maximum.
Au centre du dispositif, se trouve une source de protons, produits initialement à une vitesse nulle.
Un échappement en périphérie permet aux protons de sortir du cyclotron avec l'énergie requise.
(Le premier cyclotron français, et même européen, date de 1937, il est conservé au Musée des Arts et Métiers...
pour en savoir plus : http://pcracine.free.fr)
Document 2 :
Dans un champ magnétique
⃗
B
, une particule de masse m, de charge q, de vitesse
⃗
v
perpendiculaire à
⃗
B
subit une force de valeur
f=qvB
telle que
⃗
f
est à la fois perpendiculaire à
⃗
v
et à
⃗
B
.
Dans ces circonstances, la trajectoire de la particule chargée est circulaire, de rayon r tel que :
qvB=m v2
r
Dans un champ électrique
⃗
E
, la particule subit une force
F= ∣ q ∣ E
de même direction et de même
sens que
⃗
E
lorsque la charge de la particule est positive ; de même direction et de sens contraire
lorsque la charge est négative.

Classe de Première S  Champs et forces  Devoir à la maison 
Document 3 : le travail W d'une
force F correspond à l'énergie
transférée au système lorsque le
point d'application d'une force F
se déplace de A à B.
Le tableau ci-contre récapitule
les différentes situations.
Dans le cyclotron, ce travail sert
à accroître l'énergie cinétique du
proton,
Ec=1
2m v2
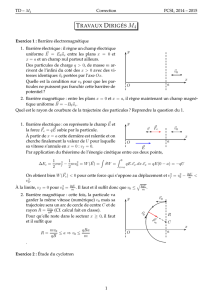
Document 4 : La tension alternative sinusoïdale.
C'est une tension alternativement
positive et négative décrite par une
sinusoïde de période T et de tension
maximale Um. Une telle tension est
utilisée pour alimenter le
condensateur du cyclotron. On peut
considérer que périodiquement, la
tension est constante et égale à Um
pendant une très courte durée quand
elle est à son maximum.
De même, la tension est considérée comme constante et égale à -Um pendant une très courte durée
quand elle est à son minimum.
Dans ce dispositif, la gravitation joue un rôle négligeable.
Questions :
2 élèves débattent vivement. Le premier prétend que la vitesse du proton devenant de plus en plus
grande, la fréquence d'inversion du champ
⃗
E
doit augmenter elle aussi. Le second affirme que la
distance parcourue par le proton dans chaque Dee augmentant, il faudra au contraire diminuer cette
fréquence. Aidez-les !
(Votre réponse sera argumentée, l'expression sera claire et concise, et le détail des calculs présenté).
Quelques pistes de réflexion :
Montrer que dans la zone de champ magnétique, la vitesse du proton est constante à chaque passage.
Calculer la durée d'un passage dans un Dee,
Exprimer le travail de la force F, celui de la force f.
Calculer l'augmentation d'énergie d'un proton à chaque traversée de la zone de coupure.
Montrer que l'augmentation d'énergie du proton dans la zone de coupure ne dépend pas de la distance
d.
Exprimer l'énergie du proton après 1 tour, 2 tours, 3 tours.
Calculer l'intensité du champ magnétique B.
Calculer le nombre de tours nécessaire à un proton pour atteindre l'énergie.