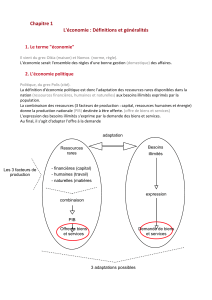
À propos de la notion d`élasticité

À propos de la notion d’élasticité
Élasticité de l’offre par rapport au prix
Fixons un bien X, notons x l’offre de ce bien (c'est-à-dire la quantité de X offerte aux
consommateurs du bien X) et px son prix unitaire.
Il est conforme au bon sens et aux usages économiques de considérer que x est une fonction
croissante de px. Plus le prix de X est élevé, plus les entreprises qui produisent X en offrent
(aux consommateurs). Jusqu’ici la quantification reste vague. Une chose importante, pour
celui qui cherche à analyser le marché du bien X, est de savoir comment l’offre varie lorsque
le prix varie.
Supposons que le prix augmente de 1% - ce qui, rappelons-le, signifie que px devient p’x = px
(1 + 1
100 ), ou encore p’x tel que, p’x–px
px = 1
100 . Il est commode et conforme à l’expérience
de l’Économie de l’offre, de modéliser la variation relative de x par une fonction linéaire de la
variation relative du prix – pour de petits accroissements. Ce qui revient à dire que le rapport
x
x
p
p
x
x
∆
∆
est constant, ce rapport est appelé l’élasticité arc de l’offre par rapport au prix. Lorsque
l’accroissement du prix tend vers 0, le rapport précédent qui s’écrit aussi ∆x
∆px × px
x , tend
vers x’(px) × px
x . C’est cette limite que les économistes appellent l’élasticité de l’offre par
rapport au prix, on la note e x
p/x .
Si l’élasticité est égale à 3, et si la variation relative du prix est de 1%, alors la variation
relative de l’offre est égale à 3×1% = 3%. On dit alors que l’offre est relativement élastique.
Si l’élasticité est égale à 0,5, alors la variation relative de l’offre est égale à 0,5 × 1% = 0,5%.
On dit que l’offre est relativement inélastique.
Une offre relativement inélastique est un phénomène souvent lié à un appareil de production
peu performant – parce que saturé ou techniquement dépassé par exemple.
Remarquez que dans le cas étudié, x étant une fonction croissante de px, x et px prenant des
valeurs positives (il s’agit de quantité de bien et de prix !), il en résulte que e > 0. Ce n’est pas
toujours le cas.
Élasticité de la demande par rapport au prix
On s’intéresse toujours au marché du bien X mais on considère maintenant la fonction de
demande, notée d. Il est naturel de la modéliser par une fonction décroissante du prix. En
général, plus un bien est cher, moins il est acheté (demandé). Il y a évidemment des
exceptions.
Avec la même définition que précédemment, e x
p/d (e en abrégé), est la limite du rapport :
x
x
p
p
d
d
∆
∆
= ∆d
∆px × px
d , quand
∆
px tend vers 0, on a donc e = d’(px)× px
d .

Ici, e est négatif et on utilise la même terminologie suivant que |e| est supérieur ou inférieur à
1.
Il est intéressant d’examiner les cas de quelques biens de consommation courante.
Considérons un bien « très » nécessaire, comme le pain par exemple. D’après vous son
élasticité, à partir de la valeur du prix en usage à un moment donné, est-elle grande ou petite ?
Autre façon de parler : la demande en pain est-elle élastique ou inélastique ?
Mêmes questions avec d’autres biens de consommation.
Et la dérivée logarithmique dans tout ça ?
Il suffit de reprendre la formule : e = d’
d
×
px, e est égale à la dérivée logarithmique de d, la
fonction de demande par rapport au prix, multipliée par px. Si d = 10
3 - 1
3 px, alors :
e =
x
p
3
1
3
10 31
−
−
× px = 10-3d
–3d . Formule qui permet de calculer l’élasticité à partir d’une valeur
de la demande. Par exemple si d = 3 (ie px = 1), alors e = - 1
9 . Si d = 7
3 (ie px=3), alors e = -
3
7 . Le modèle « renvoie » le phénomène suivant.
Lorsque le bien est bon marché, la demande est forte et inélastique. Une variation (faible
toujours) du prix n’influence guère la demande. Au contraire, si le bien est cher, il est
beaucoup moins demandé et la demande devient très élastique (une augmentation à partir du
prix déjà élevé, fait baisser très sensiblement la demande). Imaginer que le bien en question
soit le pain. À 4F (= 1 unité) la baguette, le français moyen consomme « ses » 3 baguettes par
jour (et par personne évidemment). Si le prix augmente de 10% (4,40F) il ne modifie guère
ses habitudes de consommation et celle-ci ne baisse que de 1
9
×
10%, soit à peine plus de 1%.
Si le prix de la baguette est très élevé - 12F la baguette – et si son prix augment de 10%, alors
la demande (en supposant que la fonction de demande reste la même) chute plus nettement,
exactement de 3
7 ×10 %, c’est à dire de près de 4,3 %. Ainsi même pour une demande
inélastique, la hauteur du prix est un facteur déterminant.
Élasticité de la demande par rapport aux revenus
Dans l’étude de la consommation des ménages les économistes parlent de l’élasticité-revenu.
Il s’agit toujours de la même définition, appliquée cette fois à la fonction de demande d, d’un
bien X, en fonction du revenu R. On a : e R/d = d’(R)
d(R)
×
R = ln(d(R))’
×
R.
Pour des biens « normaux » e est positive (on suppose que d est une fonction croissante de
R) : plus le revenu augmente, plus la demande est forte. Un bien normal est considéré comme
un produit de luxe, ou de confort, si e > 1. Au contraire, si son élasticité-revenu est inférieure
à 1, il est considéré comme un bien de première nécessité ou de subsistance.
Lorsque l’élasticité-revenu d’un bien est négative, il s’agit d’un bien qui conduit le
consommateur à moins consommer lorsque son revenu augmente. Un tel bien est qualifié de
bien inférieur.

Notion d’élasticité croisée
Soit 2 biens X et Y qui entretiennent des rapports « naturels » entre eux. Par exemple X =
demande de pâtes et Y = demande de riz ; ou X = demande de disques compacts et Y =
demande de lecteurs de disques compacts (les demandes font référence à une même
population). On définit l’élasticité croisée de X et de Y :
e(X,Y) = X
X∆/
Y
Y
p
p∆, où pY désigne le prix (unitaire) du bien Y. Si l’élasticité croisée est
positive les biens sont dits substituables, si l’élasticité croisée est négative les biens sont dits
complémentaires.
Remarque : dans un dossier consacré à l’utilisation de la dérivée logarithmique en section ES,
la notion d’élasticité est à évoquer. Les élèves connaissent la notion d’élasticité arc depuis la
classe de 1ère ES, il est donc tout à fait possible de proposer un exercice dans lequel on définit
la notion d’élasticité. Si j’étais examinateur à l’oral, je n’hésiterais pas à demander aux
candidats quel lien existe entre la notion d’élasticité et celle de dérivée logarithmique.