LOIS DE PROBABILITE CONTINUES A

LOIS DE PROBABILITE CONTINUES
I) LOI A DENSITE SUR UN INTERVALLE ( faire fiche '' vérifier les acquis'' )
1) Introduction
Quand l’univers est un intervalle
Jusqu’à présent, chaque expérience aléatoire conduisait à un univers fini et chaque variable aléatoire prenait un
nombre fini de valeurs.
Il s’agissait donc toujours de définir une loi de probabilité P sur un ensemble fini E = {
x1; x2;...... ;xn
}
et il suffisait de déterminer les n réels P({
x1
}) ; P({
x2
})......... P({
xn
}).
Mais il arrive aussi que les issues d’une expérience ou les résultats d’une variable aléatoire puissent être
n'importe quel nombre d’un intervalle I de ℝ. Par exemple : la durée d’une communication.
Dans ce cas, il n’est plus question de définir une loi de probabilité en se donnant la probabilité de chaque
élément de I (elle serait d’ailleurs nulle ! ) et de plus, les événement intéressants ne sont plus ’’obtenir tel ou tel
réel’’ mais plutôt ‘’ obtenir un nombre entre a et b ‘’.
La définition d’une loi de probabilité P sur I repose donc sur la notion de probabilité d’un intervalle quelconque
de I.
exemple :
On fait un sondage sur la durée des communications téléphoniques pendant un mois, puis on trace
l’histogramme et le polygone des fréquences.
La fréquence de [3;4] est l’aire du
rectangle hachuré.
Comme la somme des fréquences est 1 alors la somme des aires des rectangles est 1 UA.
Si on affine les résultats en les regroupant dans des classes de plus en plus petites, le polygone devient de plus
en plus précis.
Donc quand la largeur de la classe tend vers 0, le polygone tend vers une courbe que l’on appelle
‘’ courbe représentative de la densité de probabilité’’
La fonction f s’appelle ‘’ densité de probabilité ‘’ et l’aire hachurée est 1 UA.
La probabilité pour que la consommation soit entre a et b est donc l’aire A =
∫
a
b
fxd x
x en heure
y
010
a b
y = f(x)
A
heure
0 1 2 3 4 5 6 7 8 9 10

2) Définitions
On considère une expérience aléatoire et un univers associé  , muni d'une probabilité .
Définition 1 :
Une variable aléatoire X est dite continue si elle peut prendre toutes les valeurs
d'un intervalle I de ℝ
Ex : Durée de fonctionnement d'un appareil électrique.
Définition 2 :
Soit X une variable aléatoire continue à valeur dans un intervalle I de ℝ.
On appelle densité de probabilité sur I toute fonction f définie sur I vérifiant les trois
conditions :
- f continue sur I
- f positive sur I
-
∫
I
f(x)d x
=1
Ex : cosinus est une densité de probabilité sur [ 0 ;
2
]
Définition 3 :
On définit la loi de probabilité P de densité f de X en associant à tout intervalle [a;b] ⊂ I
le réel :
P( X ∈ [a;b]) =
∫
a
b
fxd x
On dit que P est une loi de probabilité continue à densité f sur I.
Avec notre exemple : P(X ∈[0;1]) =
∫
0
1
cosxd x
= sin(1) ≈ 0,84 et
P
(
[
π
6;π 4
]
)
=
sin
4
– sin
6
≈0,21
Définition 4 :
L'espérance d'une variable aléatoire X de densité f sur I est E(X) =
∫
I
x f (x)d x
Exercices : 36 – 33 p 382

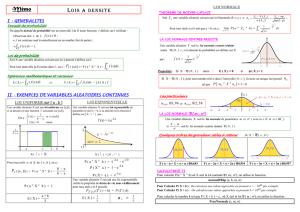
II) LA LOI UNIFORME SUR [a;b]
On dit qu'une variable aléatoire X suit la loi est uniforme sur [a;b] si sa densité est une fonction constante k.
Il faut donc k(b-a) = 1 d'où
k=1
b – a
Définition :
On appelle loi uniforme sur I = [a;b] la loi de probabilité continue sur I dont la densité f est la
fonction constante égale à
fx= 1
b–a
.
Propriété :
Si X suit la loi uniforme sur [a;b] alors pour tout intervalle [,]⊂ [a;b]
P(X ∈ [,]) =
β–α
b – a
Propriété :
Si X suit la loi uniforme sur [a;b] alors son espérance est E(X) =
a+b
2
Démo : E(X) =
∫
a
b1
b−ax d x
= …...
Exercices : 41 -42 p 383 - 4 p 367 EX 1 – 2 (feuille)

III) LES LOIS EXPONENTIELLES
Définition :
Soit  un réel strictement positif.
X suit la loi exponentielle de paramètre  sur [0 ;
+∞
[ si sa densité est la
fonction définie sur ℝ
+ par
fx= e–x
Démo : f est bien une densité car f est continue et positive et
Ia
=
∫
0
a
λe−λ xd x
=
[−e−λ x]0
a
=
1−e−λ a
et
lim
a→+∞
Ia
= 1
Propriété :
Si X suit la loi exponentielle de paramètre 
Pour tout intervalle [a;b]⊂ℝ
+ : P( X ∈ [a;b]) =
∫
a
b
λe–λxd x
=
e–λa– e–λb
et P ( X  a ) =
e−λa
Démo :
∫
a
b
λe−λ xd x
=
[−e−λ x]a
b
=
e−λa−e(−λ b)
Propriété :
L'espérance d'une variable aléatoire X qui suit la loi exponentielle de paramètre 
est E (X ) = 1/
Démo : Soit
Ia
=
∫
0
a
λx e−λ xd x
. Cherchons une primitive de la forme F(x) =
(mx+p)e−λ x
alors
F '(x)=(−λ mx−λ p+m)e−λ x
donc -m =  et -p+m = 0 donc m = -1 et p = -1/
donc
Ia
=
(
−a−1
λ
)
e−λ a
et
lim
a→+∞
Ia
= 1/.
Exercices : 6 – 9 p 369 50 - 51 p 384
Propriété :
Si X suit la loi exponentielle de paramètre  , pour tous réels positifs s et t, on a :
PXs
( X > s + t ) = P ( X > t )
On dit que la loi exponentielle est une loi de durée de vie sans vieillissement.
P ( X > a ) = P ( [ a ; +∞ [ ) =
e–a
-
lim
x∞ e–x
=
e–a
Preuve :
PXs
( X > s + t ) =
PXst∩Xs
PXs
Or ,
( X > s + t ) = ( X ∈] s + t ; + ∞ [ ) , ( X > s ) = ( X ∈] s; + ∞ [ ) et ( X ∈] s + t ; + ∞ [ ) ⊂( X ∈] s; + ∞ [ )
Donc , ( X ∈] s; + ∞ [ ) ∩ ( X ∈] s + t ; + ∞ [ ) = ( X > s + t )
D'autre part , P ( X > s + t ) =
e– λ st
et P ( X > s ) =
e– λs
insi , P ( X > s + t / X > s ) =
e– λ st
e– λs
=
e– λt
= P ( X > t )
Signification : Si par exemple X désigne la durée de vie, exprimée en années, d’un composant électronique, la
probabilité qu’il fonctionne encore t années sachant qu’il a déjà fonctionné pendant s années est la même que la
probabilité qu’il fonctionne pendant au moins t années après sa mise en service.
Remarque : Cette loi modélise le phénomène de "mort sans vieillissement", observé par exemple pour la
désintégration radioactive.

IV) LOI NORMALE CENTREE REDUITE : N (0;1)
Utiliser le fichier géogébra : '' loi binomiale '' pour expliquer ce qui suit :
Soit X une variable aléatoire qui suit une loi binomiale B(n;p). Si l'on fixe p et que l'on fait augmenter n,
l'histogramme représentant les valeurs prises par X semble se rapprocher d'une « courbe en cloche »;
Si l'on change p, la « courbe en cloche » change de caractéristiques ( hauteur et étalement)
En revanche, si on considère la variable aléatoire Z =
Z=X – x
X
=
X – np
np 1–p
, on s'aperçoit que, quel que
soit p, la courbe en cloche est toujours symétrie par rapport à l'axe des ordonnées.
De plus le mathématicien Abraham de Moivre (
XVIIe
) a montré que la courbe qui représente cette « courbe
en cloche » est la représentation de la fonction définie sur ℝ par
fx= 1
2e–x2/2
Th de MOIVRE-LAPLACE (admis)
Pour tout entier naturel n,
Xn
est une variable aléatoire qui suit la loi binomiale B( n ; p )
et on pose
Zn=Xn−np
√
np(1−p)
.
Pour tout les réels a et b (a < b) on a : la limite de
P(Zn∈[a ; b ])
quand n tend vers +
∞
est
∫
a
b1
√
2πe
−x2
2d x
Définition :
Une variable aléatoire X suit une loi normale centré réduite si sa fonction densité est la
fonction définie sur ℝ par
fx= 1
2e–x2/2
elle se note N (0;1)
Propriétés :
P(a  X  b ) =
∫
a
b
fxd x
L'aire sous la courbe est 1 : elle représente P(X ∈
]–∞;∞[
)
La courbe est symétrique par rapport à l'axe des ordonnées donc P(X
∈[0;∞[
) =
1
2
P( X  u) = P( X  -u) donc P( X  - u) = 1 – P ( X  u )