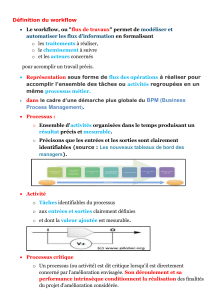
Correction de la feuille d`exercices # 1

X Y (Ω,F,P)
Y σ(X)−f:R→R
Y=f(X)Y
Y Y =Piyi1Ai
Ai∈ F Y σ(X)−Ai=Y−1(yi)∈σ(X)Bi∈ B(R)
Ai=X−1(Bi)
Y= X
i
yi1Bi!
| {z }
:=f
◦X,
f
Y
(Ω,F,P) = (]0,1[,B(]0,1[), λ)λ
X X(ω) = cos(πω)G
A⊆]0,1[ A Ac
G G ]0,1[
G
]0,1[ G=σ({x}, x ∈]0,1[)
E[X|G] = 0
G−
G∈ G E[X1G] = 0 G∈ G G
E[X1G] = ZG cos(πω)dω = 0.
G
E[X1G] = ZG cos(πω)dω =Z1
0
cos(πω)dω −ZGc cos(πω)dω = 0.

(Ω,F,P)G F X
{E(X|G)>0} G−
{X > 0}
BG− {E(X|G)>0}B
{X > 0}
E[X1Bc] = E[E(X|G)1Bc].
B X1Bc{X > 0} ∩ Bc=∅
{X > 0} ⊂ B A G− {X > 0}
A B B ∩Ac=∅B∩Ac⊂ {X= 0} G−
0 = E[X1B∩Ac] = E[E(X|G)1B∩Ac].
E(X|G)1B∩Ac= 0 B∩Ac=∅
(Ω,F,P)G F X, Y
E(X2)<+∞E(Y2)<+∞E[(X+θY )2|G]≥0p.s.
θ∈Q E[XY |G]2≤E[X2|G]E[Y2|G]p.s.
θ∈Q
E[(X+θY )2|G]≥0p.s..
Q
θ∈Q
E[X2|G]+2θE[XY |G] + θ2E[Y2|G]≥0.
θ
4E[XY |G]2−4E[X2|G]E[Y2|G]≤0,

(Ω,F,P)X
{x1, x2, . . .}Y
E[Y|X] = X
i≥1
E[Y1X=xi]
P(X=xi)1X=xi
G:= σ(X)
Gj:= {X=xj}∈G
E
X
i≥1
E[Y1X=xi]
P(X=xi)1X=xi
1Gj =E[Y1Gj],
G
Gi
X Y (Ω,F,P)
X Y g :R→R
E(g(Y)|X) = E(g(Y)) P−p.s.
X Y
gE[g(Y)] σ(X)−h
E[g(Y)h(X)] = E[g(Y)]E[h(X)] = E[E[g(Y)]h(X)],
E[g(Y)] E(g(Y)|X)
gE(g(Y)|X) = E(g(Y)) P−p.s. g =1B
h=1AA B R
E[g(Y)h(X)] = E[E[g(Y)]h(X)],
P(X∈A, Y ∈B) = P(X∈A)×P(Y∈B),
X Y
(X, Y )p(x, y) = e−y10<x<y
Y X =x X X −Y
g
E[g(Y−X)|X=x] = Z+∞
x
g(y−x)e−ydy
Z+∞
x
e−ydy
=Z+∞
x
g(y−x)e−(y−x)dy =Z+∞
0
g(u)e−udu.
xE[g(Y−X)|X]X
X Y −X