078 - IECL

078 - 1
Etudier la courbe paramétrée par
x(t) = 4
t(t+ 4) y(t) = 1 t+t−2.
Remarque : on a également
y(t) = (t−1)2
t.
Domaine de définition
La fonction xn’est pas définie en t=−4, et t= 0. La fonction yn’est pas définie en t= 0. On
a donc D=R\ {−4,0}.
Dérivées
On a facilement
x′(t) = −8(t+ 2)
t2(t+ 4)2et y′(t) = t2−1 t2.
La première dérivée s’annule en −2, et la seconde en −1et 1.
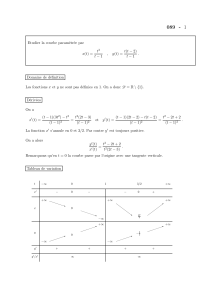
Tableau de variation
t
x′
x
y
y′
y′/x′
−∞ −4−2−1 0 1 +∞
> > q
q
q
q
:
:
:
~ ~
>
0
+∞
−∞
−1
−4
3
−∞
+∞
4
5
0
−∞
−25
4
−9
2
−4
−∞
+∞
0
+∞
+ + − −0
+− − +0 0
∞0 0

078 - 2
Asymptotes
(i) Lorsque ttend vers −4, l’abscisse xtend vers l’infini et l’ordonnée yvers −25/4. La courbe ad-
met une asymptote horizontale d’équation y=−25/4. Elle coupe l’asymptote lorsque l’ordonnée
vaut −25/4, ce qui conduit à l’équation
4(t−1)2+ 25t= 0 ,
c’est-à-dire
4t2+ 17t+ 4 = 0 .
La deuxième solution est −1/4et l’abscisse vaut alors −64/15.
(ii) Lorsque ttend vers l’infini, l’abscisse xtend vers 0et l’ordonnée yvers 0. La courbe admet
l’axe Oy comme asymptote verticale.
(iii) Lorsque ttend vers zéro, les fonctions xet ytendent vers l’infini. On a tout d’abord
y(t)
x(t)=(t−1)2(t+ 4) 4,
et cette expression tend vers 1. Ensuite
y(t)−x(t) = t2+ 2t−7
t+ 4
tend vers −7/4et la courbe admet comme asymptote la droite d’équation
y=x−7
4.
Pour étudier la position de la courbe par rapport à l’asymptote, on calcule
y(t)−x(t) + 7
4=t2+ 2t−7 t+ 4 +7 4=t(4t+ 15) t+ 4 .
Cette quantité est positive si et seulement si tappartient à l’ensemble
I= ] −4,−15/4 [ ∪] 0,+∞[,
et la courbe est au-dessus de l’asymptote si tappartient à I. Elle est en dessous dans le cas
contraire. Elle recoupe l’asymptote pour t=−15/4, ce qui donne le point de coordonnées
−64
15,−361 60 .

078 - 3
Point double
On considère le système
4
t1(t1+ 4) =4 t2(t2+ 4)
1
t1
−2 + t1=1
t2
−2 + t2
,
avec t1différent de t2.
En regroupant tous les termes dans le membre de gauche et en réduisant au même dénominateur,
on peut simplifier par t1−t2, et le système devient
t1+t2+ 4 = 0
t1t2−1 = 0 .
Si l’on pose
S=t1+t2et P=t1t2,
les nombres t1et t2sont racines du trinôme T(X) = X2−SX +P.
On peut exprimer le système en fonction de Set P.
S+ 4 = 0
P−1 = 0 .
On en déduit
P= 1 et S=−4,
Le trinôme
T(X) = X2−SX +P=X2+ 4X+ 1
a un discriminant positif et admet donc des racines réelles. On peut obtenir les valeurs de xet
ysans calculer ces racines. Si test une de ces racines, on a
t2=−4t−1.
Alors
x(t) = 4
t2+ 4t=−4 et y(t) = t2−2t+ 1 t=−6.
Le point double a donc pour coordonnées (−4,−6).

078 - 4
Tracé de la courbe
-
6
−25/4