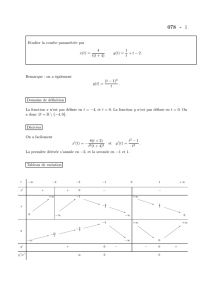
Etudier la courbe paramétrée par x(t) = t3 t − 1 , y(t) = t(t − 2) t

089 - 1
Etudier la courbe paramétrée par
x(t) = t3
t−1, y(t) = t(t−2) t−1.
Domaine de définition
Les fonctions xet yne sont pas définies en 1. On a donc D=R\ {1}.
Dérivées
On a
x′(t) = (t−1)(3t2)−t3
(t−1)2=t2(2t−3) (t−1)2et y′(t) = (t−1)(2t−2) −t(t−2) (t−1)2=t2−2t+ 2 (t−1)2.
La fonction x′s’annule en 0et 3/2. Par contre y′est toujours positive.
On a alors y′(t)
x′(t)=t2−2t+ 2 t2(2t−3) .
Remarquons qu’en t= 0 la courbe passe par l’origine avec une tangente verticale.
Tableau de variation
t
x′
x
y
y′
y′/x′
−∞ 0 1 3/2 +∞
q
q~
>
1
1
1
1
0 0− − − +
+ + + +
∞ ∞
+∞
0
−∞
+∞
27
4
+∞
−∞
0
+∞
−∞
−3
2
+∞

089 - 2
Intersection avec Ox
En dehors de 0, l’ordonnée y(t)s’annule lorsque t= 2, au point d’abscisse 8. Le coefficient di-
recteur de la tangente en ce point vaut 1/2.
Asymptote
Lorsque ttend vers 1, l’abscisse xet l’ordonnée ytendent vers l’infini. On a
y(t)
x(t)=t−2 t2,
et cette expression tend vers −1. Ensuite
y(t) + x(t) = t3+t2−2t
t−1=t2+ 2t ,
et ceci tend vers 3. La courbe admet comme asymptote la droite d’équation
y=−x+ 3 .
Pour étudier la position de la courbe par rapport à cette asymptote, on étudie le signe de
y(t) + x(t)−3 = t2+ 2t−3 = (t−1)(t+ 3) .
Cette expression est positive lorsque tappartient à l’ensemble
I1= ] −∞,−3 [ ∪] 1,+∞[.
La courbe est au-dessus de l’asymptote si tappartient à I1. Elle est en dessous dans le cas
contraire.
La courbe coupe l’asymptote si t=−3, au point de coordonnées (27/4,−15/4).
Parabole asymptote
Lorsque ttend vers l’infini, l’abscisse xet l’ordonnée ytendent vers l’infini. En écrivant
x(t) = (t3−1) + 1
t−1=t2+t+ 1 + 1 t−1et y(t) = (t−1)2−1 t−1=t−1−1 t−1,
on peut éliminer les termes en t2puis en t. En effet
y(t)2= (t−1)2−2 + 1
(t−1)2=t2−2t−1 + 1 (t−1)2,
donc
x(t)−y(t)2= 3t+ 2 + 1
t−1−1 (t−1)2,

089 - 3
puis
x(t)−y(t)2−3y(t) = 5 + 4
t−1−1 (t−1)2,
et cette expression tend vers 5. La courbe admet une parabole asymptote d’équation
x=y2+ 3y+ 5 .
Pour étudier la position de la courbe par rapport à cette parabole, on étudie le signe de
x(t)−y2(t)−3y(t)−5 = 4t−5
(t−1)2.
La courbe est à l’intérieur de la parabole lorsque tappartient à l’intervalle
I2= ] 5/4,+∞[.
La courbe coupe la parabole lorsque t= 5/4, au point de coordonnées (125/16,−15/4).
Point d’inflexion
On a
x′(t) = 2(t−1) + 3 −1
(t−1)2et y′(t) = 1 + 1 (t−1)2,
puis
x′′(t) = 2 + 2
(t−1)3et y′′(t) = −2 (t−1)3,
et l’on en déduit
x′(t)y′′(t)−y′(t)x′′(t) = −2tt2−3t+ 6
(t−1)3.
Le seul point d’inflexion possible est donc en t= 0.
Point double
On considère le système
t3
1
t1−1=t3
2
t2−1
t1(t1−2)
t1−1=t2(t2−2) t2−1
,
avec t1différent de t2.
En regroupant tous les termes dans le membre de gauche et en réduisant au même dénominateur,
on peut simplifier par t1−t2, et le système devient
(t1+t2)t1t2−(t2
1+t1t2+t2
2) = 0
t1t2−(t1+t2) + 2 = 0 .

089 - 4
Si l’on pose
S=t1+t2et P=t1t2,
les nombres t1et t2sont racines du trinôme T(X) = X2−SX +P.
On peut exprimer le système en fonction de Set P.
SP −S2+P= 0
P−S+ 2 = 0 .
En remplaçant Ppar S−2dans la première équation, on obtient
−S−2 = 0 ,
d’où
P=−4 et S=−2.
Le trinôme
T(X) = X2−SX +P=X2+ 2X−4
a un discriminant positif et admet donc des racines réelles. On peut obtenir les valeurs de xet
ysans calculer ces racines. Si test une de ces racines, on a
t2=−2t+ 4 ,
donc
t3=−2t2+ 4t= 8t−8 et t2−2t−=−4t+ 4 .
Alors
x(t) = 8 et y(t) = −4.
Le point double a donc pour coordonnées (8,−4).

089 - 5
Tracé de la courbe
-
6
3