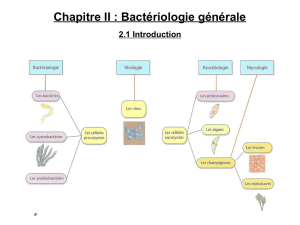
ET3

Problème : Etude du projet de transport dans des capsules sous vide (Evacuated Tube transport, ET3), pour un Paris-
New York via l’Inde, la Chine et le Détroit de Béring en 6 heures.
(Thème : vitesse, accélération, fonction linéaire, somme des termes d’une suite arithmétique)
Les capsules ET3, qui pèsent 180 kg à vide et qui peuvent contenir 4 à 6 passagers, sont propulsées dans des tubes
presque sous vide, donc avec très peu de frottements aérodynamiques. Ces capsules sont en sustentation magnétique
ce qui annule les frottements mécaniques. L’accélération des capsules, d’environ 1 g soit environ 10 m/s² (ou 10 m/s
par s), est réalisée grâce à une série de moteurs électriques en début de trajet. La capsule continue sa route toute
seule (moteurs quasiment arrêtés) une fois sa vitesse de croisière atteinte.
Ce système devrait permettre de voyager à 6480 km/h en consommant 50 fois moins d’énergie qu’un train classique.
1) A 6480 km/h, quelle durée (en heure et min) serait nécessaire pour parcourir 40 000 km (soit environ la longueur
de l’équateur) ?
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
2) a) Avec l’accélération constante de 10 m/s², la vitesse de la capsule augmente de 10 m/s à chaque seconde.
Exprimez alors la vitesse de la capsule (en m/s) en fonction du temps t (en s) sachant que cette vitesse vaut 0 pour t =
0 : v(t) = ……………
b) Exprimez 6480 km/h en m/s : ………………………………………………………………
c) Quelle durée sera nécessaire pour faire passer la vitesse d’une capsule de 0 à 6480 km/h ?
……………………………………………..
d) Représenter graphiquement la vitesse v(t) de la capsule en fonction du temps t avec un logiciel ou votre
calculatrice.
e) Quel type de courbe représente la vitesse v en fonction du temps ? …………………………..
www.et3.com
1

3) Calcul de la distance nécessaire pour l’accélération de 0 à 1800 m/s.
Durant la 1ère seconde de la phase d’accélération, la capsule passe de 0 à 10 m/s et y a donc une vitesse moyenne de
5 m/s. Elle parcourt donc 5 m durant cette 1ère seconde.
Durant la 2ème seconde de la phase d’accélération, la capsule passe de 10 à 20 m/s et y a donc une vitesse moyenne
de 15 m/s. Elle parcourt donc 15 m durant cette 2ème seconde.
Durant la 3ème seconde de la phase d’accélération, la capsule passe de 20 à 30 m/s et y a donc une vitesse moyenne
de 25 m/s. Elle parcourt donc 25 m durant cette 3ème seconde.
Et ainsi de suite… La distance parcourue pendant une seconde augmente de 10 m à chaque seconde.
a) Compléter la phrase :
Les distances parcourues par la capsule chaque seconde : 5 m ; 10 m ; 15 m ; … constituent les termes d’une suite
………….. de raison …..
b) A l’aide d’un tableur, calculer la distance totale d (en m) parcourue par la capsule durant les ………. s de la phase
d’accélération :
d = ……………………………………………………………………………………….. d’après le tableur
c) Calculer la distance parcourue pendant la 180ème s de la phase d’accélération :
u180 = ………………
Retrouver la distance totale d parcourue par la capsule durant les … s de la phase d’accélération à l’aide de la
formule donnant la somme des termes de la suite.
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………
2

Corrigé
1) A 6480 km/h, quelle durée (en heure et min) serait nécessaire pour parcourir 40 000 km (soit la longueur de
l’équateur) ?
6,17 h soit 6 h 10 min
2) a) Avec l’accélération constante de 10 m/s², la vitesse de la capsule augmente de 10 m/s à chaque seconde.
Exprimez alors la vitesse de la capsule (en m/s) en fonction du temps t (en s) sachant que cette vitesse vaut 0 pour t =
0 : v(t) = 10.t
b) Exprimez 6480 km/h en m/s : 1800 m/s
c) Quelle durée sera nécessaire pour faire passer la vitesse d’une capsule de 0 à 6480 km/h ?
180 s soit 3 min
d) Représenter graphiquement la vitesse v(t) de la capsule en fonction du temps t avec un des logiciels Geogebra,
Sinequanon ou Excel.
e) Quel type de courbe représente la vitesse v en fonction du temps ? une droite linéaire
3) Calcul de la distance nécessaire pour l’accélération de 0 à 1800 m/s.
a) Compléter la phrase :
Les distances parcourues par la capsule chaque seconde : 5 m ; 10 m ; 15 m ; … constituent les termes d’une suite
arithmétique de raison 10.
b) A l’aide d’un tableur, calculer la distance totale d (en m) parcourue par la capsule durant les 180 s de la phase
d’accélération :
d = 162 000 m d’après le tableur
c) Retrouver la distance totale d parcourue par la capsule durant les 180 s de la phase d’accélération à l’aide de la
formule donnant la somme des termes de la suite.
u180 = 5 + 10 × 179 = 1795 m
d = 180.(u1 + u 180)/2 = 180.(5 + 1795) = 180 × 900 = 162 000 m soit 162 km.
(rmq : d = aire du triangle = 180 × 1800/2 = 162 000 m
ou d = 0,5 a t² = 0,5 × 10 × 180² = 162 000 m)
v(t) en m/s
t en s
3