Proportionnalité

Proportionnalité
1. Définition
Définition :
un tableau est un tableau de proportionnalité lorsque tous les nombres d'une ligne s'obtiennent en
multipliant tous ceux de l'autre ligne par un même nombre.
Ce dernier nombre est appelé coefficient de proportionnalité.
exemple 1 :
Ce tableau est un tableau de proportionnalité. Les quotients sont tous égaux :
4 est le coefficient de proportionnalité.
exemple 2 :
Ce tableau n'est pas un tableau de proportionnalité. Les quotients ne sont pas égaux.
Propriété :
Lorsqu’on a un tableau de proportionnalité, pour passer d’une ligne à l’autre, on multiplie par
le même nombre (dans l’exemple 1, c’est 4) : le coefficient de proportionnalité. Mais pour
faire le chemin inverse, on multiplie aussi par un nombre toujours le même, mais qui est
différent du premier. Dans l’exemple 1, pour faire le chemin inverse, on multiplie par ¼ (ce
qui revient à diviser par 4).
De manière générale, si dans un sens le coefficient de proportionnalité est a, dans le chemin
inverse c’est l’inverse de a : 1/a.
Propriété :
Si y est proportionnel à x, comme dans le tableau ci-dessous :
x -2 3 1 4
y -5 7,5 2,5 10
Et l’on place les points de coordonnées (x ; y) dans un graphique, ces points sont alignés avec
l’origine O(0 ;0). La réciproque est vraie : si en plaçant les points d’un tableau dans un
graphique on constate qu’ils sont alignés avec l’origine, c’est que le tableau est un tableau de
proportionnalité.
On dit que y est une fonction linéaire de x (on reverra cela plus tard).

2. Quatrième proportionnelle
Dans le tableau de proportionnalité ci-dessous, trouver le quatrième nombre :
x = = 35
35 est la quatrième proportionnelle.
Autre exemple :
A
C
B
Pour trouver la quatrième proportionnelle, on cherche le coefficient de proportionnalité pour passer
de la ligne 1 à la ligne 2. C’est
B
A
. On multiplie alors par C pour trouver le nombre à mettre dans la
case vide : c’est :
BC
A×
=
BC
A
. C’est la règle pour trouver la quatrième proportionnelle.
3. Utilisation de la proportionnalité
Il y a énormément de situation physiques où la proportionnalité doit être utilisée :
- Pour les conversions de grandeurs : transformer des mètres en kilomètres, des litres en
décilitres, …
- Pour les grandeurs définies par des produits ou des quotients.
Ex : la masse est proportionnelle au volume quand on choisit un corps particulier, et toutes
choses égales par ailleurs (T°, pression,…). Le coefficient de proportionnalité s’appelle la
masse volumique du corps. 1 Litre d’eau pèse environ 1 Kg, 3L d’eau pèsent 3 Kg, etc… La
masse volumique de l’eau est d’environ 1Kg/L (dans les conditions usuelles).
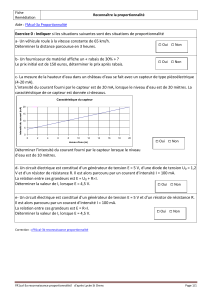
Ex : En électricité, aux bornes d’un résistor, on a U = RI. La tension est proportionnelle à
l’intensité du courant, et le coefficient de proportionnalité s’appelle la résistance du résistor.
Pour une résistance de 3 V/A (volt par ampère), pour un courant de 0,1 A, on a une tension
de 3 V. Pour un courant de 0,5 A, on a une tension de 1,5 V. Habituellement, les V/A (Volts
par ampères) sont appelés Ohms (Ω). C’est l’unité que l’on utilise pour les résistances.
Il y a beaucoup d’autres exemples de lois physiques ou chimiques de ce type.
- Il y a encore beaucoup d’autres cas où la proportionnalité doit être utilisée.
Mais attention ! Ce n’est pas toujours le cas ! Si y dépend seulement de x, y n’est pas forcément
proportionnel à x !! Ex : l’aire d’un carré par rapport à la longueur de son côté, l’énergie cinétique en
fonction de la vitesse (formule : E = ½ m v². Le carré fait que ce n’est pas proportionnel), etc.
Les journalistes font souvent l’erreur de langage de dire que 2 grandeurs sont proportionnelles
uniquement parce que lorsque l’une augmente, l’autre augmente aussi. La proportionnalité, ce n’est
pas ça (en fait c’est la définition d’une fonction croissante, pas linéaire) ; la proportionnalité c’est
plutôt : quand je double une des deux grandeurs, l’autre double aussi.