TD5 corrigeÌ

TD5 corrigé - Partie 1
Corrigé des premiers exercices
(1.1, 1.2, 1.4, 2.1 et 2.4)
1. Mise en route
1.1 Chute libre, « mouvement naturel » et force
Depuis l’antiquité, et jusqu’à encore peu de temps avant Newton (avec Galilée), la chute libre est
considérée comme un mouvement naturel, c’est-à-dire un mouvement ayant lieu de lui-même, qui
ne nécessite pas d’action d’une force s’exerçant sur l’objet en chute libre.
Dans l’expérience courante en effet, le phénomène de chute est omniprésent, il peut avoir lieu pour
(quasiment) tous types d’objet, quelles que soient les circonstances. Ce n’est pas le cas par exemple
du mouvement lié à l’attraction d’un aimant, qui ne concerne que certains objets, et que l’on peut
faire cesser simplement en retirant l’aimant. Le fait que dans l’expérience courante la chute ait
toujours lieu et qu’elle concerne tous les objets, indépendamment des circonstances, légitime le fait
de la considérer comme une tendance naturelle des objets, comme ce fut le cas pendant si
longtemps dans l’histoire des idées.
a) Qu’est-ce qui, dans la dynamique de Newton (défini par les trois lois du mouvement), mène
à interpréter le mouvement de chute libre en termes de force ? Quel est le mouvement que
l’on pourrait considérer comme naturel dans cette théorie ?
La première loi de Newton, ou principe d’inertie, pose que le mouvement rectiligne uniforme n’est pas interprété
en termes de force. Ce qui revient à le considérer comme un mouvement naturel, au sens défini précédemment
(« un mouvement ayant lieu de lui-même, qui ne nécessite pas d’action d’une force s’exerçant sur l’objet »).
Cela pose ainsi une première définition du concept de force dans la théorie de Newton : on parlera de force
s’exerçant sur un objet lorsque son mouvement est différent du mouvement rectiligne uniforme. Ou autrement
dit, toute déviation du mouvement naturel posé par le principe d’inertie sera interprétée en termes de force.
Ainsi pour le cas de la chute libre, c’est l’augmentation de la vitesse au cours de la chute
qui implique de l’interpréter en termes de force : c’est un mouvement différent du
mouvement rectiligne uniforme. Même s’il y avait de très bonnes raisons de considérer la
chute libre comme un mouvement naturel, c’est la définition d’un autre mouvement
naturel dans la théorie de Newton (suggérés par d’autres observations expérimentales),
qui implique de changer de définition du concept de force et d’interpréter alors la chute
libre comme associée à une force.
b) A partir uniquement de la description du mouvement d’un objet, quelle est la grandeur
physique qui caractérise en un point donné la présence d’une force (résultante) s’exerçant
sur cet objet ? Donner son expression explicite (à partir de la variation du vecteur vitesse).

Il s’agit du vecteur accélération :    
. En effet, un mouvement rectiligne uniforme correspond
formellement à un vecteur vitesse constant,    , ce qui implique également que le vecteur variation du
vecteur vitesse soit nulle :  . Ainsi un mouvement différent du mouvement rectiligne signifie  . Pour
définir la « déviation » du vecteur vitesse en un point, on fait tendre vers zéro l’intervalle de temps entre lequel
on compare les deux vecteurs vitesse (le  apparaissant dans      ). Ce qui amène à définir
le vecteur accélération :    
 .
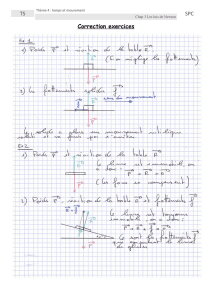
c) On considère le mouvement d’une pierre ayant été jetée
(1) verticalement vers le haut, au cours de sa phase montante et
(2) de façon oblique, le long de sa trajectoire parabolique.
(cf. schémas représentant les positions et vecteurs vitesse à différents instants)
Dans chacun des cas :
- A priori, quelle(s) force(s) s’exerce(nt) sur la pierre ? (on néglige la présence de l’air)
- A partir de la figure, comment déterminer la direction de la force (résultante) qui s’exerce
sur la pierre ?
- En comparant avec la figure correspondant à la chute vers le bas, que peut-on dire sur les
forces dans les différents cas, au niveau de leur direction et de leur intensité ?
Dans la mécanique de Newton, le concept de force est définit à partir de vecteur accélération, par la deuxième
loi du mouvement :
Donc la direction du vecteur force est donné par la direction du vecteur accélération. Or en première
approximation, pour un  suffisamment court, l’accélération vaut  
, elle est donc dans la direction de la
variation du vecteur vitesse,  .
On peut le voir sur le schéma de synthèse suivant :

Ainsi, pour déterminer la direction de la force dans les différents exemples, à partir des schémas du
mouvements, il s’agit de déterminer construire le vecteur  , pour déterminer sa direction :
Le fait que les variations de vecteurs vitesse soient identiques dans les trois cas indique que l’accélération est la
même, en supposant que l’intervalle de temps entre les différents vecteurs vitesse représentés soit identique
dans les trois cas. Autrement dit, même  , même , donc même  
 (en première approximation, pour
un intervalle de temps suffisamment court). Et donc puisqu’il s’agit du même objet à chaque fois, on a
également même masse , donc même force : 
 .
Donc la même force s’exerce sur la pierre à la montée, à la descente, ou sur une trajectoire parabolique (la
masse étant identique).
 On voit donc que des trajectoires différentes peuvent être associées à un même vecteur accélération, et
donc à une même force.
 Il n’y a pas nécessairement une force dans le sens du mouvement.
1.2 Décomposition de la force résultante
a) A partir de la détermination de l’accélération, on a accès uniquement à la force résultante
s’exerçant sur un objet. S’il est soumis à plusieurs actions, comment est-ce possible de
décomposer cette force résultante en ses différentes composantes, correspondant à
chacune des actions ?
Ce n’est pas possible avec une seule expérience. Il faut avoir plusieurs mises en situation où les différentes
interactions sont présentes individuellement. En effet si on se souvient du principe de superposition des forces la
composante d’accélération d’un objet due à une force est la même en présence ou non d’autres forces. Une
force déterminée dans un certain contexte expérimental est la même dans un autre contexte expérimental où
d’autres forces sont présentes. Lorsqu’on fait un « bilan des forces », on suppose qu’on connait déjà à l’avance
les forces en jeu, que l’on a pu déterminer antérieurement à partir du mouvement, avec d’autres expériences.
b) Un parachutiste a sauté d’un avion, son parachute est ouvert, et il tombe à une vitesse
constante V. Que vaut la force résultante qui s’exerce sur lui ?
Comment trouver la valeur de la force due à la présence du parachute, ?
La détermination des différentes composantes de force s’exerçant sur lui nécessite un autre contexte
expérimental où elles ne sont pas toutes présentes. En particulier, on peut considérer le cas où le parachutiste
n’ouvre pas son parachute. Dans ce cas, (en première approximation) il tombe avec une accélération constante

, et est donc soumis à la force   . Lorsque le parachute est ouvert, la force résultante qui
s’exerce sur lui est nulle (en effet, il est à vitesse constante donc son accélération est nulle). Si on suppose que le
parachutiste ne subit que son poids  et la force 
 qu’on cherche ici, on a donc 
soit 
 .
On a supposé implicitement que la force qui s’exerce indépendamment du parachute ( ) est la même
dans le cas avec le parachute, il s’agit du principe de superposition.
c) On constate expérimentalement que si la masse du parachutiste est plus grande, la vitesse
limite du parachutiste augmente proportionnellement (en première approximation). Que
peut-on en conclure pour modéliser la force  liée à la résistance de l’air dans le parachute ?
Si 
 , l’observation   , (c’est-à-dire     , où C est une constante), implique que   .
Donc la force de résistance de l’air dans le parachute, lorsque le parachutiste a atteint sa vitesse limite , est
proportionnelle à cette vitesse limite. D’autre part cette force est dirigée vers le haut (selon ), soit dans la
direction opposée au mouvement, soit dans la direction opposée au vecteur vitesse. On peut donc écrire :

1.4 Principe d’action réciproque 1
Deux étudiants en physique, un fainéant et un pragmatique, doivent pousser leur voiture en panne.
Ils font les commentaires suivants :
(1) : « D’après la troisième loi de Newton, le principe d’action-réaction, si on exerce une force sur la
voiture, elle exerce une force d’intensité égale dans la direction opposée. Il est donc impossible de
faire avancer la voiture de toute manière. »
(2) : « En poussant suffisamment, l’action devient plus forte que la réaction et on peut bien faire
avancer la voiture. »
Expliquer pourquoi ils se trompent tous les deux.
A l’aide d’un schéma, proposer une analyse correcte de la situation, lorsque la voiture est en
mouvement. (Suggestion : représenter les différents systèmes concernés séparément, ainsi que
l’ensemble des interactions en jeu)
L’ambiguïté est due au fait que le point de contact entre les mains qui poussent et la voiture appartient aux
deux systèmes à la fois : le pousseur et la voiture. Ce qui crée une confusion sur le système sur lequel s’exerce
chacune des forces. Une façon de lever cette ambigüité est de séparé abstraitement les deux systèmes, afin de
faire bien apparaitre, pour chaque force, sur quel système elle s’applique.
On peut ainsi faire apparaitre chaque couple « action – réaction » de la même couleur, qui s’exerce toujours sur
des systèmes différents. Ainsi la force du pousseur sur la voiture s’applique sur la voiture, et la réaction de la
voiture sur le pousseur s’exerce sur le pousseur. Et donc lorsqu’on fait le bilan des forces sur la voiture, on ne
considère que la force du pousseur sur la voiture. L’action et la réaction ne peuvent jamais faire partie d’un
même bilan des forces pour un système, puisque elles s’exercent sur deux systèmes différents !
(extait de « Raisonner en physique », Viennot 1996)