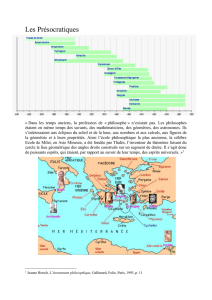
Document

Un peu de culture !
Thalès, l'homme de l'ombre
Appuyé au bastingage, Thalès regardait s'éloigner la terre d'Ionie où jusqu'à ce jour il avait vécu.
Milet disparu dans le lointain, il partait pour l'Egypte.
Poussé par les vents étésiens qui ne soufflent qu'en été durant les périodes de canicule, le navire
accomplit la traversée d'une traite, arriva en vue des côtes égyptiennes, pénétra dans le lac Mariotis
où Thalès s'embarqua sur une felouque qui devait remonter le Nil.
Après quelques jours d'un voyage interrompu par de nombreux arrêts dans les villes bordant le fleuve,
il l'aperçut. Dressée au milieu d'un large plateau, non loin de la rive, la pyramide de Khéops !
Thalès n'avait jamais rien vu d'aussi
imposant. Deux autres pyramides,
Khéphren et Mykérinos, s'élevaient
sur le plateau; à côté , elles
paraissaient petites et pourtant…
Tout au long du voyage sur le Nil, les
voyageurs l'avaient pourtant averti.
Les dimensions du monument
dépassaient tout ce qu'il avait imaginé.
Thalès quitta la felouque. A mesure
qu'il s'approchait, sa marche se fit
plus lente; comme si le monument, par
sa seule masse, parvenait à ralentir ses
pas. Il s'assit, vaincu. Un fellah
sans âge s'assit à ses côtés.
"Sais-tu, étranger, combien de mort à
coûté cette pyramide que tu sembles
admirer?""Des milliers sans doute." "Dis des dizaines de milliers." "Des dizaines de milliers !" "Dis des
centaines de milliers." "Des centaines de milliers !" Thalès le regarda incrédule.
"Plus, peut-être, ajouta le fellah. Pourquoi tant de mort ? Pour creuser un canal ? retenir un fleuve ?
Construire une route ? Bâtir un palais ? Dresser un temple en l'honneur des Dieux ? Tu n'y es pas ! Le
pharaon Khéops a dressé cette pyramide dans le seul but d'obliger les humains à se persuader de leur
petitesse. La construction devait excéder toute norme pour nous accabler: plus gigantesque elle serait,
plus infime nous serions. Le but est atteint. Le pharaon et ses architectes ont voulu nous contraindre
d'admettre qu'entre cette pyramide et nous il n'y a aucune mesure !"
Ainsi depuis 2000 ans, cet édifice construit pourtant par la main des hommes restait hors de portée de
leur connaissance. Quels qu'aient été les buts de Pharaon, il restait une évidence: la hauteur de la
pyramide était impossible à mesurer. Elle était la construction la plus visible du monde habité et elle
était la seule à ne pouvoir être mesurée ! Thalès voulut relever le défi.
Toute la nuit Thalès et le fellah discutèrent.
Lorsque le soleil éclaira l'horizon, Thalès se leva. Il regarda sa propre ombre se déployer en direction
de l'ouest; il pensa que quelle que soit la petitesse d'un objet, il existe toujours un éclairage qui le fait
grand. Longtemps, il resta debout, immobile, les yeux fixés sur la tâche sombre que faisait son corps
sur le sol. Il la vit rapetisser à mesure que le soleil s'élevait dans le ciel.
"Puisque ma main ne peut effectuer la mesure, ma pensée l'effectuera."
Thalès fixa longtemps la pyramide.
« le rapport que j'entretiens avec mon ombre est le
même que celui que la pyramide entretient avec la sienne »
D'après «le théorème du perroquet», Denis Guedj, 1998
Résume ce texte en 5 lignes maximum

2,44m
9,15m
20m
h
B
E
C
F
A
EXERCICE 1
Le joueur s’apprête à tirer un coup franc à 20m du but. Le gardien de but adverse a placé un mur de joueurs à 9,15m du ballon.
Le tireur va tirer le ballon si fort que sa trajectoire sera considérée comme rectiligne.
Pour chacune des questions, faire un schéma en précisant les dimensions que tu connais et celle que tu cherches.
a. Quelle devrait être la taille maximale des joueurs
composant le mur pour que le tir soit cadré ?
b. Si les joueurs mesuraient 1,80m, combien devrait
mesurer la cage pour que le tir soit cadré ?
c. A quelle distance du but devrait se trouver le tireur si
le mur mesure 1,80m et la cage 2,44m ?
EXERCICE 2
Dans ce problème, l’unité de longueur est le centimètre et l’unité d’aire est le cm².
La figure ci-dessous est donnée à titre d’exemple pour préciser la disposition des points. Ce n’est pas une figure en vraie
grandeur.
ABC est un triangle tel que :
AC = 20 cm
BC = 16 cm
AB = 12 cm
F est un point du segment [BC]
La perpendiculaire à la droite (BC) passant par F coupe [CA] en E.
On a représenté sur la figure le segment [BE].
Première partie.
1. Démontrer que le triangle ABC est rectangle en B.
2. Calculer son aire.
3. Démontrer, en s’aidant de la question 1. , que la droite (EF) est parallèle à la droite (AB)
Deuxième partie.
On se place dans le cas où CF = 4 cm.
1. Démontrer que EF = 3 cm.
2. Calculer l’aire du triangle EBC
EXERCICE 3 Effectuer les calculs suivants :
(Tu peux utiliser ta calculatrice, mais tu dois écrire au minimum une étape dans ton calcul)
a)
1
23
1
32
b)
14
3
24
3
c)
51
2
1
41