Vincent Berthet - 03-11-2015

Vincent Berthet - 03-11-2015
Maître de Conférences - http://vincentberthet.com
Vincent Berthet
Maître de Conférences
PDF generated March 11, 2015 by Kalin's PDF Creation Station WordPress plugin
1 / 14

Vincent Berthet - 03-11-2015
Maître de Conférences - http://vincentberthet.com
Table Of Contents
L’inférence bayésienne, probablement descriptive, certainement normative ............. 3
2 / 14

Vincent Berthet - 03-11-2015
Maître de Conférences - http://vincentberthet.com
L’inférence bayésienne, probablement descriptive, certainement
normative
by Vincent Berthet - mercredi, mars 11, 2015
http://vincentberthet.com/linference-bayesienne-probablement-descriptive-certainement-normative/
En 1763, était publiée à titre posthume une lettre intitulée An Essay towards solving a Problem in the
Doctrine of Chances [1]. Son auteur, le révérend et mathématicien anglais Thomas Bayes (1702-1761), y
démontrait un théorème fondamental en théorie des probabilités. Aujourd’hui, ce théorème est devenu
une norme de la pensée inférentielle.
D’UNE FORMULE MATHÉMATIQUE...
La formule de Bayes porte sur la notion de probabilité conditionnelle. Petit rappel (je reprends ici un
exemple posté sur l’excellent blog sciencetonnante).
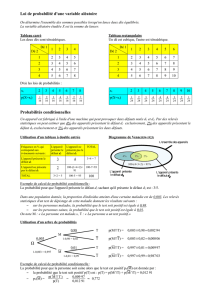
Une urne est composée de 60 carrés (dont 51 bleus et 9 rouges) et 40 triangles (dont 4 bleus et 36
rouges). On tire au hasard un objet dans l’urne.
Une probabilité simple est par exemple celle d’obtenir un carré :
Une probabilité conditionnelle est par exemple celle d’obtenir un carré sachant que l’objet est de couleur
rouge. Il y a 45 objets rouges dont 9 sont des carrés, donc :
On voit que la probabilité « l’objet est un carré sachant qu’il est rouge » (20%) est très inférieure à la
probabilité « l’objet est un carré » (60%). La notion de probabilité conditionnelle exprime le fait que la
probabilité simple d’un événement est susceptible d’être modifiée par l’ajout d’une information.
Considérons maintenant la probabilité conditionnelle d’obtenir un objet de couleur rouge sachant que
3 / 14

Vincent Berthet - 03-11-2015
Maître de Conférences - http://vincentberthet.com
c’est un carré. Il y a 60 carrés dans l’urne dont 9 sont rouges, donc :
Si l’on compare les deux probabilités P(Carré | Rouge) et P(Rouge | Carré), on voit qu’elles ont en
commun l’élément P(Rouge ? Carré). On peut ainsi les mettre en relation dans une même formule. En
observant que :
on a :
Il s’agit de la formule de Bayes. Son intérêt est de montrer comment on passe d’une probabilité
conditionnelle à la probabilité conditionnelle symétrique. Sa formulation générale est la suivante :
Prenez le temps de contempler cette formule mathématique légendaire...
4 / 14

Vincent Berthet - 03-11-2015
Maître de Conférences - http://vincentberthet.com
Source: wikipedia.
Dans le cas particulier de deux événements exhaustifs et mutuellement exclusifs A1, A2, on note que :
donc :
Dans notre exemple :
A1 : l’objet est un carré
A2: l’objet est un triangle
B : l’objet est rouge
5 / 14